
| A. | -2 | B. | -4 | C. | -8 | D. | 不能确定 |
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:选择题
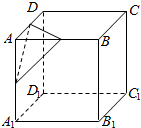 如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )| A. | 此多面体的表面积为$\frac{47}{8}$a2 | B. | 体对角线AC1垂直于截面 | ||
| C. | 截面平行于平面CB1D1 | D. | 有10个顶点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某高三毕业班甲、乙两名同学在连续的8次数学周练中,统计解答题失分的茎叶图如下:
某高三毕业班甲、乙两名同学在连续的8次数学周练中,统计解答题失分的茎叶图如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
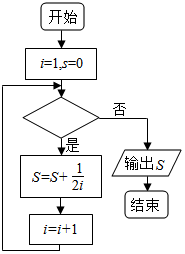
| A. | i≤1007 | B. | i≤1008 | C. | i>1008 | D. | i>1007 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com