
 ij������ҵ��ס�������ͬѧ��������8����ѧ�����У�ͳ�ƽ����ʧ�ֵľ�Ҷͼ���£�
ij������ҵ��ס�������ͬѧ��������8����ѧ�����У�ͳ�ƽ����ʧ�ֵľ�Ҷͼ���£����� ��1���ֱ�����ס���������Ա�ĵ÷־�ֵ�ͷ���ɴ�����������
��2��X�����п���ȡֵΪ0��1��2��������X��B��2��$\frac{3}{16}$�����ɴ������X�ķֲ��к�EX��
��� �⣺��1��$\overline{{x}_{��}}$=$\frac{1}{8}$��7+9+11+18+18+16+23+28��=15��
$\overline{{x}_{��}}$=$\frac{1}{8}$��7+8+10+15+17+19+21+23��=15��
${{S}_{��}}^{2}$=$\frac{1}{8}$[��-8��2+��-6��2+��-4��2+��-2��2+��-2��2+12+82+132]=44.75��
${{S}_{��}}^{2}$=$\frac{1}{8}$[��-8��2+��-7��2+��-5��2+02+22+42+62+82]=32.25��
�ס���������Ա�ĵ÷־�ֵ��ȣ��ķ�����ҵķ����
����ͬѧ��������ȶ�Щ��
��2������ͳ�ƽ������һ�������У�����ʧ�ֳ���15�ֵĸ��ʷֱ���${p}_{1}=\frac{3}{8}$��${p}_{2}=\frac{1}{2}$��
����ʧ�־�����15�ֵĸ���Ϊp1p2=$\frac{3}{16}$��
X�����п���ȡֵΪ0��1��2��������X��B��2��$\frac{3}{16}$����
P��X=0��=${C}_{2}^{0}��\frac{13}{16}��^{2}$=$\frac{169}{256}$��
P��X=1��=${C}_{2}^{1}��\frac{3}{16}����\frac{13}{16}��$=$\frac{78}{256}$��
P��X=2��=${C}_{2}^{2}��\frac{3}{16}��^{2}$=$\frac{9}{256}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{169}{256}$ | $\frac{78}{256}$ | $\frac{9}{256}$ |
���� ���⿼��ƽ�������������������ɢ����������ķֲ��С���ѧ�����������е��⣬����ʱҪ�������⣬ע�����ֲ������ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �ڢ� | C�� | �٢� | D�� | �ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -4 | C�� | -8 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | i��7 | B�� | i��7 | C�� | i��9 | D�� | i��9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
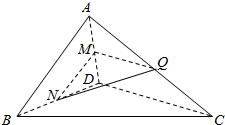 ��ͼ����������ABCD�У�AB��CD��AB��AD��M��N��Q�ֱ�Ϊ��AD��BD��AC���е㣮
��ͼ����������ABCD�У�AB��CD��AB��AD��M��N��Q�ֱ�Ϊ��AD��BD��AC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | sinx | B�� | cosx | C�� | -sinx | D�� | -cosx |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com