
| A. | $({\frac{4π}{3},0})$ | B. | $({\frac{π}{2},0})$ | C. | $({\frac{π}{3},0})$ | D. | $({\frac{π}{6},0})$ |
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,m∥β,则 n∥β | B. | 若m∥β,α⊥β,则 m⊥α | ||
| C. | 若m∥n,m⊥β,则n⊥β | D. | 若m?α,n?β,α∥β,则 n∥m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
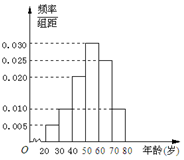 广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
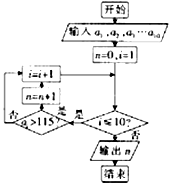 某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )
某旅游景点统计了今年5月1号至10号每天的门票收入(单位:万元),分别记为a1,a2,…,a10(如:a3表示5月3号的门票收入),表是5月1号到5月10号每天的门票收入,根据表中数据,下面程序框图输出的结果为( )| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 门票收入(万元) | 80 | 120 | 110 | 91 | 65 | 77 | 131 | 116 | 55 | 77 |
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com