
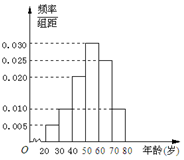
 广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.分析 (1)由频率分布直方图能求出这40名广场舞者中年龄分布在[40,70)的人数.
(2)由直方图能求出这组数据的众数和中位数.
(3)由直方图可知,年龄在[20,30)有2人,分别记为a1,a2,在[30,40)有4人,分别记为b1,b2,b3,b4,利用列举法能求出从这6人中任选两人,这两名广场舞者中恰有一人年龄在[30,40)的概率.
解答 解:(1)由表中数据知,
这40名广场舞者中年龄分布在[40,70)的人数为(0.02+0.03+0.025)×10×40=30
(2)由直方图可知这组数据的众数为55
因为(0.005+0.01+0.02+0.015)×10=0.5,
故中位数为55.
(3)由直方图可知,年龄在[20,30)有2人,分别记为a1,a2,
在[30,40)有4人,分别记为b1,b2,b3,b4,
现从这6人中任选两人,共有如下15种选法:
(a1,a2),(a1,b1),(a1,b2),(a1,b3),(a1,b4),(a2,b1),
(a2,b2),(a2,b3),(a2,b4),(b1,b2),(b1,b3),(b1,b4),
(b2,b3),(b2,b4),(b3,b4),
其中恰有1人在[30,40)有8种,
故这两名广场舞者中恰有一人年龄在[30,40)的概率为p=$\frac{8}{15}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{3}{4}$π) | B. | ($\frac{π}{3}$,$\frac{3}{4}$π] | C. | ($\frac{π}{4}$,$\frac{π}{3}$] | D. | [$\frac{π}{3}$,$\frac{3}{4}$π)∪($\frac{π}{4}$,$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
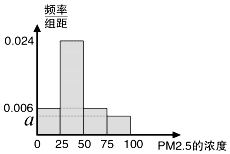 根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:
根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如表:| 组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
| 第一组 | (0,25] | 3 | 0.15 |
| 第二组 | (25,50] | 12 | 0.6 |
| 第三组 | (50,75] | 3 | 0.15 |
| 第四组 | (75,100] | 2 | 0.1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{4π}{3},0})$ | B. | $({\frac{π}{2},0})$ | C. | $({\frac{π}{3},0})$ | D. | $({\frac{π}{6},0})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
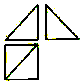 如图,一个几何体的三视图如图所示(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为a的正方形,则其外接球的体积为( )
如图,一个几何体的三视图如图所示(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为a的正方形,则其外接球的体积为( )| A. | $\frac{{\sqrt{3}}}{2}π{a^3}$ | B. | $\frac{{\sqrt{3}}}{2}a$ | C. | $\frac{1}{2}{a^3}$ | D. | $\frac{1}{2}π{a^3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.
如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com