
 如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.
如图,在三棱锥A-BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点.分析 (1)取AB中点E,则EQ∥PC,从而EQ∥平面CPM,由中位线定理得DE∥PM,从而DE∥平面CPM,由此能证明DQ∥平面CPM.
(2)法1:推导出AD⊥CM,BD⊥CM,从而CM⊥平面ABD,进而得到∠CPM是二面角C-AB-D的平面角,由此能求出∠BDC的正切值.
法2:以M为坐标原点,MC,MD,ME所在的直线分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出∠BDC的正切值.
解答 证明:(1)取AB的中点E,则$\frac{AE}{EP}$=2=$\frac{AQ}{QC}$,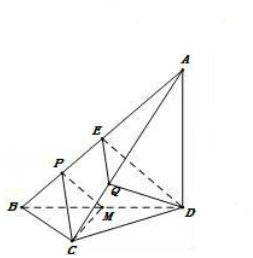
∴EQ∥PC,
又EQ?平面CPM,∴EQ∥平面CPM,
又PM是△BDE的中位线,∴DE∥PM,
从而DE∥平面CPM,∴平面DEQ∥平面CPM,
∴DQ∥平面CPM.
解:(2)解法1:由AD⊥平面BCD,知AD⊥CM,
由BC=CD,BM=MD,知BD⊥CM,
故CM⊥平面ABD,
由(1)知DE∥PM,而DE⊥AB,故PM⊥AB,
∴∠CPM是二面角C-AB-D的平面角,∴∠CPM=$\frac{π}{3}$,
设PM=a,则CM=$\sqrt{3}a$,DM=BM=$\sqrt{2}a$,
在Rt△CMD中,tan∠MDC=$\frac{MC}{MD}$=$\frac{\sqrt{3}a}{\sqrt{2}a}$=$\frac{\sqrt{6}}{2}$,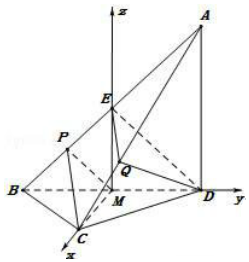
∴tan∠BDC=$\frac{\sqrt{6}}{2}$.
解法2:以M为坐标原点,MC,MD,ME所在的直线分别为x轴,y轴,z轴,
建立空间直角坐标系,
设MC=a,MD=b,则C(a,0,0),B(0,-b,0),A(0,b,2b),
则$\overrightarrow{BC}$=(a,b,0),$\overrightarrow{BA}$=(0,2b,2b),
设$\overrightarrow{n}$=(x,y,z)是平面ABC的一个法向量,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BC}=ax+by=0}\\{\overrightarrow{n}•\overrightarrow{BA}=2by+2bz=0}\end{array}\right.$,取x=b,得$\overrightarrow{n}$=(b,-a,a),
平面ABD的一个法向量$\overrightarrow{m}$=(1,0,0),
∵二面角C-AB-D的大小为$\frac{π}{3}$,∴cos$\frac{π}{3}$=|cos<$\overrightarrow{n},\overrightarrow{m}$>|=$\frac{|\overrightarrow{n}•\overrightarrow{m}|}{|\overrightarrow{n}|•|\overrightarrow{m}|}$=$\frac{b}{\sqrt{{b}^{2}+2{a}^{2}}}$=$\frac{1}{2}$,
整理得:$\frac{a}{b}=\frac{\sqrt{6}}{2}$,
在Rt△CMD中,tan∠MDC=$\frac{MC}{MD}=\frac{b}{a}=\frac{\sqrt{6}}{2}$,
∴tan∠BDC=$\frac{\sqrt{6}}{2}$.
点评 本题考查线面垂直的证明、角的正切、二面角等基础知识,考查推理论证能力、运算求解能力、空间想象能力、数据处理能力,考查函数与方程思想、化归与转化思想、数形结合,考查创新意识、应用意识,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
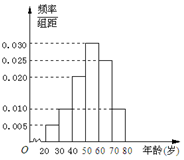 广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2,\frac{5π}{6})$ | B. | $(2,\frac{11π}{6})$ | C. | $(2,\frac{4π}{3})$ | D. | $(2,\frac{5π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
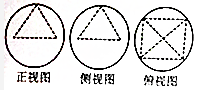
| A. | 18 | B. | 9 | C. | 9$\sqrt{2}$ | D. | 18$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com