
分析 利用诱导公式进行化简求值即可.
解答 解:由$sin({α-\frac{7π}{2}})=-\frac{1}{5}$得:cosα=-$\frac{1}{5}$.
∵α为第三象限角,
∴sinα=-$\frac{2\sqrt{6}}{5}$
∴$\frac{{sin({π-α})cos({2π-α})tan({\frac{3π}{2}-α})}}{{cot({-3π-α})sin({-\frac{π}{2}-α})}}$=$\frac{sinα•cosα•cotα}{-cotα•(-cosα)}$=sinα=-$\frac{2\sqrt{6}}{5}$.
故答案是:-$\frac{2\sqrt{6}}{5}$.
点评 本题主要考察了同角三角函数关系式和诱导公式的应用,属于基本知识的考查.


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{15}{16}$ | B. | $\frac{15}{8}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若ea+2a=eb+3b,则a>b | B. | 若ea+2a=eb+3b,则a<b | ||
| C. | 若ea-2a=eb-3b,则a>b | D. | 若ea-2a=eb-3b,则a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
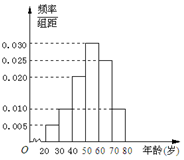 广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,也是城市精神文明建设成果的一个重要象征.2016年某校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
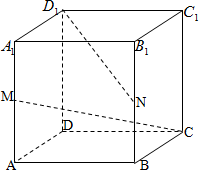 正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:
正方体ABCD-A1B1C1D1中,M、N分别为棱A1A和B1B的中点.求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com