
 如图,在正方体ABCD-A1B1C1D1中,棱AB=1,点E、F分别为AB、BC的中点.
如图,在正方体ABCD-A1B1C1D1中,棱AB=1,点E、F分别为AB、BC的中点.分析 (1)根据直线平面垂直的性质,判定转化证明线线垂直.
(2)连接B1H,由等腰三角形“三线合一”的性质可得EF⊥BH,由正方体的几何特征,可得B1H⊥EF,则∠B1HB是二面角B1-EF-B的平面角,解三角形B1HB,即可得到二面角B1-EF-B的大小
(3)根据体积公式V=$\frac{1}{3}$×S△BEF×BB1,先求解面积,高线问题.
解答  (1)证明:连结AC、BD,AC与BD交于点O.
(1)证明:连结AC、BD,AC与BD交于点O.
∵DD1⊥AD,DD1⊥AC,AD∩DC=D
∴DD1⊥平面ABCD.
∴DD1⊥AC,
又四边形是正方形,AC⊥BD,BD∩DD1=D
∴AC⊥平面BDD1.
∴AC⊥BD1
∵点E、F分别是AB、BC的中点
∴EF∥AC,
∴EF⊥BD1,
(2)解:EF与BD相交于点H,连接B1H,∵E、F分别是AB、BC的中点,∴EF⊥BH
又BB1⊥平面ABCD,∴BH是B1H在平面ABCD的射影,∴B1H⊥EF
∴∠B1HB是二面角B1-EF-B的平面角,
∴tan∠B1HB=$\frac{{B}_{1}B}{BH}$=$\frac{{B}_{1}B}{\frac{1}{4}×\sqrt{2}{B}_{1}B}$=2$\sqrt{2}$;
(3)解:∵AB=1.BB1⊥平面ABCD,
∴BB1是三棱锥B1-BEF的高,
∵AB⊥BC,E,F,分别是AB,CD的中点.
∴S△BEF=$\frac{1}{2}×BE$×BF=$\frac{1}{8}$,
∴V=$\frac{1}{3}×$S△BEF×BB1=$\frac{1}{24}$.
点评 本题考查了直线平面的位置关系,运用定理判断位置关系,求解大小,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
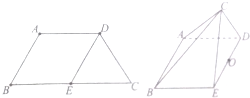 如图,ABCD为等腰梯形,且AD∥BC,E为BC的中点,AB=AD=BE,沿DE将△CDE折起成四棱锥C-ABED.
如图,ABCD为等腰梯形,且AD∥BC,E为BC的中点,AB=AD=BE,沿DE将△CDE折起成四棱锥C-ABED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,AA1=4,P是棱BB1上一点,BP=3,且PA1⊥PC.
如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB=$\sqrt{3}$,AA1=4,P是棱BB1上一点,BP=3,且PA1⊥PC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com