
分析 根据双曲线C的渐近线方程,设出双曲线的方程,代入点(2,2 $\sqrt{2}$),即可求得C的标准方程.然后求解双曲线C的准线方程.
解答 解:由题意,∵双曲线C的渐近线方程为y=±2x,
∴设双曲线C的方程为y2-4x2=λ
∵双曲线C经过点(2,2$\sqrt{2}$),
∴8-16=λ
∴λ=-8
∴双曲线C的方程为y2-4x2=-8,即$\frac{{x}^{2}}{2}-\frac{{y}^{2}}{8}=1$,a=$\sqrt{2}$,c=$\sqrt{10}$,
双曲线C的准线方程:$x=±\frac{{\sqrt{10}}}{5}$.
故答案为:$x=±\frac{{\sqrt{10}}}{5}$.
点评 本题考查双曲线的标准方程,考查双曲线的几何性质,考查学生的计算能力,属于中档题.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
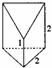 如图是底面边长为2,高为2的正三棱柱除去上面的一个高为1的三棱锥后剩下的部分构成的几何体的直观图,则该几何体的体积为$\frac{5\sqrt{3}}{3}$.
如图是底面边长为2,高为2的正三棱柱除去上面的一个高为1的三棱锥后剩下的部分构成的几何体的直观图,则该几何体的体积为$\frac{5\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
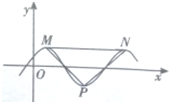 函数f(x)=$\frac{1}{2}$sin($\frac{1}{2}$ωx+$\frac{π}{6}$)(ω>0,)x∈R的部分图象如图所示,设M,N是图象上的最高点,P是图象上的最低点,若△PMN为等腰直角三角形,则ω=2π.
函数f(x)=$\frac{1}{2}$sin($\frac{1}{2}$ωx+$\frac{π}{6}$)(ω>0,)x∈R的部分图象如图所示,设M,N是图象上的最高点,P是图象上的最低点,若△PMN为等腰直角三角形,则ω=2π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com