
已知函数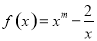 且
且 ,
,
(1)求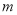 的值;
的值;
(2)判断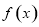 在
在 上的单调性,并用定义给予证明.
上的单调性,并用定义给予证明.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2015届甘肃省高二下学期期末考试理科数学试卷(解析版) 题型:解答题
假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少?
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知命题p: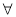 x∈R,x2+x-6
x∈R,x2+x-6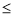 0,则命题
0,则命题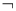 P是( )
P是( )
A.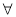 x∈R,x2+x-6>0 B.
x∈R,x2+x-6>0 B.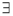 x∈R.x2+x-6>0
x∈R.x2+x-6>0
C.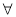 x∈R,x2+x-6>0 D.
x∈R,x2+x-6>0 D.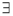 x∈R.x2+x-6<0
x∈R.x2+x-6<0
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知函数
(1)若函数 在
在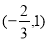 上单调递减,在
上单调递减,在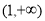 上单调递增,求实数
上单调递增,求实数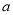 的值;
的值;
(2)是否存在实数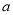 ,使得
,使得 在
在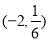 上单调递减,若存在,试求
上单调递减,若存在,试求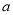 的取值范围;
的取值范围;
若不存在,请说明理由;
(3)若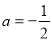 ,当
,当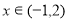 时不等式
时不等式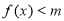 有解,求实数
有解,求实数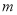 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期末考试文科数学试卷(解析版) 题型:选择题
已知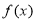 是定义在
是定义在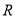 上的偶函数,且
上的偶函数,且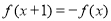 ,若
,若 在
在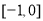 上单调递减,则
上单调递减,则 在
在 上是( )
上是( )
A.增函数 B.减函数
C.先增后减的函数 D.先减后增的函数
查看答案和解析>>
科目:高中数学 来源:2015届甘肃省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
用1,2,3,4,5组成没有重复数字的五位数,其中有且仅有一个偶数夹在两个奇数之间的五位数的个数为
A.36 B.48 C.72 D.120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com