
分析 利用an=Sn-Sn-1求出数列{an}的通项公式,然后利用${a_n}=3{log_2}{b_n}-2({n∈{N^*}})$,求出数列{bn}通项公式;利用cn=anbn.求出数列cn的通项公式,写出前n项和Tn的表达式,利用错位相减法,求出前n项和Tn.
解答 解:由已知得,当n≥2时,an=Sn-Sn-1=($\frac{3}{2}$n2-$\frac{1}{2}$n)-[$\frac{3}{2}$(n-1)2-$\frac{1}{2}$(n-1)]=3n-2,
又a1=1=3×1-2,符合上式.
故数列{an}的通项公式an=3n-2.
又因为${a_n}=3{log_2}{b_n}-2({n∈{N^*}})$,
所以log2bn=$\frac{1}{3}$(an+2)=n,即bn=2n,
令cn=anbn.
则cn=(3n-2)•2n.
所以Tn=1×21+4•22+7•23+…+(3n-2)•2n,①
2Tn=1×22+4×23+7•24+…+(3n-2)•2n+1,②
由②-①得:-Tn=2+3•22+3•23+…+(3n-5)•2n+1=3×(2+22+…+2n)-(3n-2)•2n+1-2
=-(3n-5)•2n+1-10,
所以Tn=10+(3n-5)2n+1
故答案是:10+(3n-5)2n+1.
点评 本题考查数列的通项公式的求法,数列求和等基础知识,考查计算能力、推理论证能力、综合发现问题解决问题的能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $({0,\frac{1}{2}})$ | B. | $({0,\frac{{\sqrt{2}}}{4}})$ | C. | $({\frac{{\sqrt{2}}}{4},\frac{1}{2}})$ | D. | $({\frac{1}{2},1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 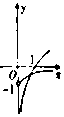 | C. | 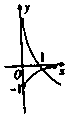 | D. | 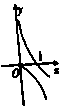 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)+g(x)是奇函数 | B. | f(x)-g(x)是偶函数 | C. | f(x)•g(x)是奇函数 | D. | f(x)•g(x)是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com