
| A. | ac<bc | B. | abc<bac | C. | ca<cb | D. | logac<logbc |
分析 根据幂函数的单调性和条件判断A和B,根据指数函数的单调性判断C,根据对数函数的单调性和对数的运算性质判断D.
解答 解:A、因为0<c<1,所以函数y=xc在(0,+∞)上递增,
又a>b>1,则ac>bc,A不正确;
B、因为0<c<1,所以c-1<0,函数y=xc-1在(0,+∞)上递减,
又a>b>1,则ac-1<bc-1,两边同除以ab可得:abc>bac,B不正确;
C、因为0<c<1,所以函数y=cx在定义域上递减,
又a>b>1,则cb>ca,C正确;
D、因为0<c<1,所以函数$y=lo{g}_{c}^{x}$在(0,+∞)上递减,
又a>b>1,则$lo{g}_{c}^{a}<lo{g}_{c}^{b}<0$,即$\frac{1}{lo{g}_{c}^{a}}>\frac{1}{lo{g}_{c}^{b}}$,
所以$lo{g}_{a}^{c}>lo{g}_{b}^{c}$,D不正确,
故选:C.
点评 本题考查了幂函数、指数函数、对数函数的单调性,以及对数运算性质的应用,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{5}$ | C. | $\sqrt{17}$ | D. | $\sqrt{17}$或$\frac{\sqrt{17}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
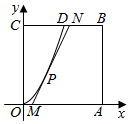 某地要建造一个边长为2(单位:km)的正方形市民休闲公园OABC,将其中的区域ODC开挖成一个池塘,如图建立平面直角坐标系后,点D的坐标为(1,2),曲线OD是函数y=ax2图象的一部分,对边OA上一点M在区域OABD内作一次函数y=kx+b(k>0)的图象,与线段DB交于点N(点N不与点D重合),且线段MN与曲线OD有且只有一个公共点P,四边形MABN为绿化风景区:
某地要建造一个边长为2(单位:km)的正方形市民休闲公园OABC,将其中的区域ODC开挖成一个池塘,如图建立平面直角坐标系后,点D的坐标为(1,2),曲线OD是函数y=ax2图象的一部分,对边OA上一点M在区域OABD内作一次函数y=kx+b(k>0)的图象,与线段DB交于点N(点N不与点D重合),且线段MN与曲线OD有且只有一个公共点P,四边形MABN为绿化风景区:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com