
分析 根据奇函数的定义判断①,根据函数的图象判断②③④
解答 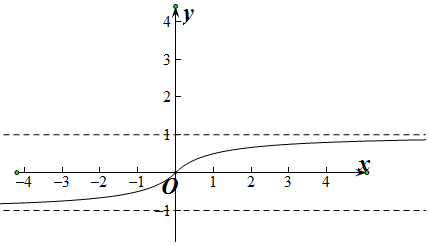 解:f(x)=$\frac{x}{1+|x|}$(x∈R)的图象为
解:f(x)=$\frac{x}{1+|x|}$(x∈R)的图象为
对于①,函数的定义域为R,f(-x)=$\frac{-x}{1+|-x|}$=-$\frac{x}{1+|x|}$=-f(x),
f(x)+f(-x)=0恒成立,故①正确,
对于②,由图象可知,函数的值域为(-1,1),
故存在m∈(0,1),使得方程|f(x)|=m有两个不等实数根,故②正确,
对于③由图象可知,函数在R上单调递增,故任意x1,x2∈R,若x1≠x2,则一定有f(x1)≠f(x2),故③正确,
对于④,分别画出y=f(x)与y=kx的图象,由图象可知,使得函数g(x)=f(x)-kx在R上有一个零点,故④错误,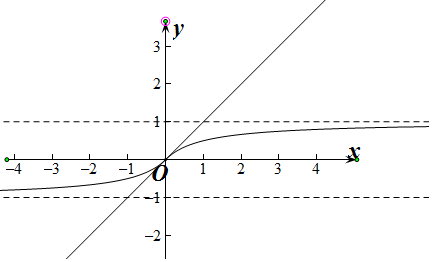
故答案为:①②③
点评 本题考查了函数图象及其性质,关键是绘制函数图象,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{10}$ | C. | 4 | D. | $\sqrt{34}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,lgx=0 | B. | ?x∈R,sinx+cosx=$\sqrt{3}$ | ||
| C. | ?x∈R,x2+1≥2x | D. | ?x∈R,2x>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
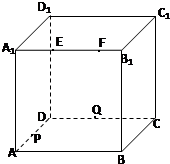 如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:
如图,正方体ABCD一A1B1C1D1的棱长为2,动点E,F在棱A1B1上,且EF=1,动点Q在棱CD上,P是棱AD中点,R是棱DDl的中点,则以下结论:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com