
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .直角梯形
.直角梯形![]() 可以通过直角梯形
可以通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且平面
为轴旋转得到,且平面![]() 平面
平面![]() .
.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2017/12/20/1842736631291904/1845869604462592/STEM/592e486e595e40bf846fae2bfa16ac59.png]
(I)求证: ![]() .
.
(II)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)设![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 上的点(都不与点
上的点(都不与点![]() 重合).若直线
重合).若直线![]() 平面
平面![]() ,求
,求![]() 的长.
的长.
【答案】(I)见解析;(II)![]() ;(III)
;(III)![]() .
.
【解析】试题分析:(I)由面面垂直定理得![]() 面
面![]() ,由线面垂直定理即可得出
,由线面垂直定理即可得出![]() .
.
(II)以A为原点建立空间直角坐标系,设平面![]() 的一个法向量为
的一个法向量为![]() ,令
,令![]() ,
, ![]() ,即可求出直线
,即可求出直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)设![]() ,由
,由![]() ,表示
,表示![]() ,
, ![]() ,
,
由![]() ,,求得
,,求得![]() ,,即可求出MH的长.
,,即可求出MH的长.
试题解析:(I)∵![]() ,
,
∴![]() ,
,
∵平面![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]() ,
,
∴![]() 面
面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.
(II)由(I)知, ![]() 平面
平面![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
如图,以![]() 为原点建立空间直角坐标系,
为原点建立空间直角坐标系,
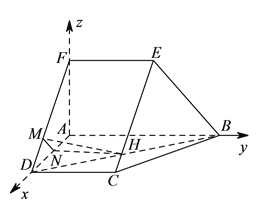
∵![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() ,
, ![]() ,
,
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
∵![]() ,
,
![]() ,
,
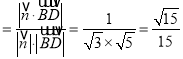 .
.
(III)在以![]() 为原点的空间直角坐标系中,
为原点的空间直角坐标系中,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() .
.
设![]() ,
,
![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
若![]() 平面
平面![]() ,
,
则![]() ,即
,即![]() ,
,
![]() ,解得
,解得![]() ,
,
∴![]() ,
,
![]() .
.
点睛:高考对空间向量与立体几何的考查主要体现在以下几个方面:①求异面直线所成的角,关键是转化为两直线的方向向量的夹角;②求直线与平面所成的角,关键是转化为直线的方向向量和平面的法向量的夹角;③求二面角,关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键.


科目:高中数学 来源: 题型:
【题目】甲、乙两人进行射击比赛,各射击![]() 局,每局射击
局,每局射击![]() 次,射击命中目标得
次,射击命中目标得![]() 分,未命中目标得
分,未命中目标得![]() 分,两人
分,两人![]() 局的得分情况如下:
局的得分情况如下:
甲 |
|
|
|
|
乙 |
|
|
|
|
(Ⅰ)若从甲的![]() 局比赛中,随机选取
局比赛中,随机选取![]() 局,求这
局,求这![]() 局的得分恰好相等的概率.
局的得分恰好相等的概率.
(Ⅱ)如果![]() ,从甲、乙两人的
,从甲、乙两人的![]() 局比赛中随机各选取
局比赛中随机各选取![]() 局,记这
局,记这![]() 局的得分和为
局的得分和为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
(Ⅲ)在![]() 局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出![]() 的所有可能取值.(结论不要求证明)
的所有可能取值.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:
①将![]() ,
, ![]() ,
, ![]() 三种个体按3:1:2的比例分层抽样调查,若抽取的
三种个体按3:1:2的比例分层抽样调查,若抽取的![]() 个体为12个,则样本容量为30;
个体为12个,则样本容量为30;
②一组数据1、2、3、4、5的平均数、中位数相同;
③甲组数据的方差为5,乙组数据为5、6、9、10、5,那么这两组数据中较稳定的是甲;
④统计的10个样本数据为95,105,114,116,120,120,122,125,130,134,则样本数据落在![]() 内的频率为0.4.
内的频率为0.4.
其中真命题为( )
A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是等腰三角形,
是等腰三角形,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 上一点.
上一点.
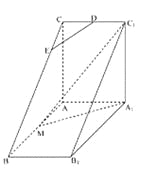
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 将三棱柱
将三棱柱![]() 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区中学生的身体发育状况,拟采用分层抽样的方法从甲、乙、丙三所中学抽取![]() 个教学班进行调查.已知甲、乙、丙三所中学分别有
个教学班进行调查.已知甲、乙、丙三所中学分别有![]() ,
, ![]() ,
, ![]() 个教学班.
个教学班.
(Ⅰ)求从甲、乙、丙三所中学中分别抽取的教学班的个数.
(Ⅱ)若从抽取的![]() 个教学班中随机抽取
个教学班中随机抽取![]() 个进行调查结果的对比,求这
个进行调查结果的对比,求这![]() 个教学班中至少有一个来自甲学校的概率.
个教学班中至少有一个来自甲学校的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),将
),将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后得到
个单位长度后得到![]() 的图象,且
的图象,且![]() 在区间
在区间![]() 内的最大值为
内的最大值为![]() .
.
(1)求实数![]() 的值;
的值;
(2)在![]() 中,内角
中,内角![]() ,
, ![]() ,
, ![]() 的对边分别是
的对边分别是![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 的周长
的周长![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,过其右焦点
,过其右焦点![]() 与长轴垂直的直线与椭圆在第一象限相交于点
与长轴垂直的直线与椭圆在第一象限相交于点![]() ,
, ![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,右顶点为
,右顶点为![]() ,点
,点![]() 是椭圆上的动点,且点
是椭圆上的动点,且点![]() 与点
与点![]() ,
, ![]() 不重合,直线
不重合,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,直线
,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,求证:以线段
,求证:以线段![]() 为直径的圆恒过定点.
为直径的圆恒过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com