
【题目】为了解某地区中学生的身体发育状况,拟采用分层抽样的方法从甲、乙、丙三所中学抽取![]() 个教学班进行调查.已知甲、乙、丙三所中学分别有
个教学班进行调查.已知甲、乙、丙三所中学分别有![]() ,
, ![]() ,
, ![]() 个教学班.
个教学班.
(Ⅰ)求从甲、乙、丙三所中学中分别抽取的教学班的个数.
(Ⅱ)若从抽取的![]() 个教学班中随机抽取
个教学班中随机抽取![]() 个进行调查结果的对比,求这
个进行调查结果的对比,求这![]() 个教学班中至少有一个来自甲学校的概率.
个教学班中至少有一个来自甲学校的概率.
【答案】(Ⅰ)![]() ,
, ![]() ,
, ![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(Ⅰ)先求出甲、乙、丙三所中学的教学班所占比例,用样本容量乘以甲、乙、丙三所中学的教学班所占比例,即得从甲、乙、丙三所中学中分别抽取的教学班的个数.
(Ⅱ)由(Ⅰ)知,从甲、乙、丙三所中学分别抽取2,1,3个教学班,不妨分别记为 A1,A2,B1,C1,C2,C3,把从6个教学班中随机抽取2个教学班的基本事件一一列举
出来,找出其中至少有1个来自甲学校的基本事件,即可求出这2个教学班中至少有1个来自甲学校的概率.
试题解析:
(Ⅰ)由已知可知在甲、乙、丙三所中学,
共有教学楼之比为![]() ,
,
∴甲、乙、丙三所中学教学班所占比例分别为![]() ,
, ![]() ,
, ![]() .
.
甲: ![]() 个,
个,
乙: ![]() 个,
个,
丙: ![]() 个.
个.
∴分别抽取甲、乙、丙教学班![]() ,
, ![]() ,
, ![]() 个.
个.
(Ⅱ)设从甲抽取![]() 个教学班为
个教学班为![]() 、
、![]() ,
,
从乙抽取![]() 个教学班为
个教学班为![]() ,
,
从丙抽取![]() 个教学班为
个教学班为![]() ,
, ![]() ,
, ![]() .
.
则从![]() 个班中抽取
个班中抽取![]() 个班的基本事件为:
个班的基本事件为: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 一共有
一共有![]() 个.
个.
设“从![]() 个班抽
个班抽![]() 个班,至少有一个来自甲校”为事件
个班,至少有一个来自甲校”为事件![]() ,则事件
,则事件![]() 包含的基本事件如下
包含的基本事件如下![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共
共![]() 个,
个,
∴![]() ,
,
故从![]() 个班中抽
个班中抽![]() 个班,至少有一个来自甲校的概率为
个班,至少有一个来自甲校的概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中, ![]() 为坐标原点,曲线
为坐标原点,曲线![]() :
:  (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,有相同单位长度的极坐标系中,直线
轴的正半轴为极轴,有相同单位长度的极坐标系中,直线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求与直线![]() 平行且与曲线
平行且与曲线![]() 相切的直线的直角坐标方程。
相切的直线的直角坐标方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型娱乐场有两种型号的水上摩托,管理人员为了了解水上摩托的使用及给娱乐城带来的经济收入情况,对该场所最近6年水上摩托的使用情况进行了统计,得到相关数据如表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
使用率 | 11 | 13 | 16 | 15 | 20 | 21 |
(1)请根据以上数据,用最小二乘法求水上摩托使用率![]() 关于年份代码
关于年份代码![]() 的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
的线性回归方程,并预测该娱乐场2018年水上摩托的使用率;
(2)随着生活水平的提高,外出旅游的老百姓越来越多,该娱乐场根据自身的发展需要,准备重新购进一批水上摩托,其型号主要是目前使用的Ⅰ型、Ⅱ型两种,每辆价格分别为1万元、1.2万元.根据以往经验,每辆水上摩托的使用年限不超过四年.娱乐场管理部对已经淘汰的两款水上摩托的使用情况分别抽取了50辆进行统计,使用年限如条形图所示:
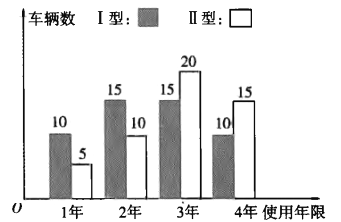
已知每辆水上摩托从购入到淘汰平均年收益是0.8万元,若用频率作为概率,以每辆水上摩托纯利润(纯利润![]() 收益
收益![]() 购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
购车成本)的期望值为参考值,则该娱乐场的负责人应该选购Ⅰ型水上摩托还是Ⅱ型水上摩托?
附:回归直线方程为![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .直角梯形
.直角梯形![]() 可以通过直角梯形
可以通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且平面
为轴旋转得到,且平面![]() 平面
平面![]() .
.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2017/12/20/1842736631291904/1845869604462592/STEM/592e486e595e40bf846fae2bfa16ac59.png]
(I)求证: ![]() .
.
(II)求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
(III)设![]() 为
为![]() 的中点,
的中点, ![]() ,
, ![]() 分别为线段
分别为线段![]() ,
, ![]() 上的点(都不与点
上的点(都不与点![]() 重合).若直线
重合).若直线![]() 平面
平面![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com