
分析 根据三角形的重心的性质及向量加法平行四边形法则、向量数乘的几何意义,根据条件进行向量数量积的运算即可求出
解答 解:根据重心的性质,$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\frac{1}{3}$($\overrightarrow{CA}$+$\overrightarrow{CB}$),($\overrightarrow{OA}$+$\overrightarrow{OC}$)=$\frac{1}{3}$($\overrightarrow{BA}$+$\overrightarrow{BC}$)=$\frac{1}{3}$($\overrightarrow{CA}$-$\overrightarrow{CB}$-$\overrightarrow{CB}$)=$\frac{1}{3}$($\overrightarrow{CA}$-2$\overrightarrow{CB}$),
又|$\overrightarrow{CA}$|=|$\overrightarrow{CB}$|=1,∠BCA=60°;
∴($\overrightarrow{OA}$+$\overrightarrow{OB}$)•($\overrightarrow{OA}$+$\overrightarrow{OC}$)=$\frac{1}{9}$($\overrightarrow{CA}$+$\overrightarrow{CB}$)($\overrightarrow{CA}$-2$\overrightarrow{CB}$)=$\frac{1}{9}$(${\overrightarrow{CA}}^{2}$-$\overrightarrow{CA}•\overrightarrow{CB}$-2${\overrightarrow{CB}}^{2}$)=$\frac{1}{9}$(1-$\frac{1}{2}$-2)=-$\frac{1}{6}$,
故答案为:-$\frac{1}{6}$.
点评 考查三角形重心的概念及性质,等边三角形的概念,向量加法的平行四边形法则,向量数乘的几何意义,以及向量的数乘运算,向量数量积的运算及计算公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
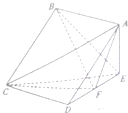 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 75° | B. | 75°或105° | C. | 45° | D. | 45°或135° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e1•e2>1 | B. | e1•e2<1 | ||
| C. | e1•e2=1 | D. | e1•e2与1大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com