
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
分析 在三角形ABC内部取一点P,要满足S△PBC≤$\frac{1}{3}$S△ABCP点应位于图中DE(DE∥BC并且AD:AB=2:3)的下方,然后用阴影部分的面积除以原三角形的面积即可得.
解答 解:记事件A={△S△PBC≤$\frac{1}{3}$S△ABC},基本事件是三角形ABC的面积,(如图)
事件A的几何度量为图中阴影部分的面积(DE∥BC并且AD:AB=2:3),
因为阴影部分的面积是整个三角形面积的($\frac{2}{3}$)2=$\frac{4}{9}$,
所以P(A)=1-$\frac{阴影部分面积}{三角形面积}=1-\frac{4}{9}=\frac{5}{9}$;
故选:C.
点评 本题考查了几何概型,解答此题的关键在于明确测度比是面积比.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a,b与α所成的角相等,则a∥b | B. | 若a∥α,b∥β,α∥β,则a∥b | ||
| C. | 若a?α,b?β,a∥b,则α∥β | D. | 若a⊥b,a⊥α,b?α,则b∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
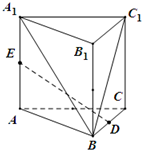 在棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,CA=CB=CC1=2,∠ACB=90°,D,E分别是线段BC,AA1的中点.
在棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,CA=CB=CC1=2,∠ACB=90°,D,E分别是线段BC,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com