
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月储蓄![]() 对月收入
对月收入![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判断变量![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
其中![]() ,
,![]() 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为![]()
附:线性回归方程![]() 中,
中,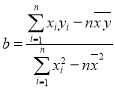 ,
,![]() ,
,
科目:高中数学 来源: 题型:
【题目】过曲线C1:![]() -
-![]() =1(a>0,b>0)的左焦点F1作曲线C2:x2+y2=a2的切线,设切点为M,直线F1M交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若|MF1|=|MN|,则曲线C1的离心率为( )
=1(a>0,b>0)的左焦点F1作曲线C2:x2+y2=a2的切线,设切点为M,直线F1M交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若|MF1|=|MN|,则曲线C1的离心率为( )
A. ![]() B.
B. ![]() -1 C.
-1 C. ![]() +1 D.
+1 D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是( )
①平均数![]() ≤3;②标准差S≤2;③平均数
≤3;②标准差S≤2;③平均数![]() ≤3且标准差S≤2;④平均数
≤3且标准差S≤2;④平均数![]() ≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
≤3且极差小于或等于2;⑤众数等于1且极差小于或等于1.
A.①② B.③④
C.③④⑤ D.④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9 元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85(元/km)).
(1)将某乘客搭乘一次出租车的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆出租车行驶8 km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们知道,如果集合AS,那么S的子集A的补集为SA={x|x∈S,且xA}.类似地,对于集合A、B,我们把集合{x|x∈A,且xB}叫作集合A与B的差集,记作A-B.据此回答下列问题:
(1)若A={1,2,3,4},B={3,4,5,6},求A-B;
(2)在下列各图中用阴影表示集合A-B.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x-3|-|x+1|,x∈R.
(1)解不等式f(x)<-1;
(2)设函数g(x)=|x+a|-4,且g(x)≤f(x)在x∈[-2,2]上恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业拟生产一种如图所示的圆柱形易拉罐(上下底面及侧面的厚度不计).易拉罐的体积为![]()
![]() ,设圆柱的高度为
,设圆柱的高度为![]()
![]() ,底面半径为
,底面半径为![]()
![]() ,且
,且![]() .假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为
.假设该易拉罐的制造费用仅与其表面积有关.已知易拉罐侧面制造费用为![]() 元/
元/ ![]() ,易拉罐上下底面的制造费用均为
,易拉罐上下底面的制造费用均为![]() 元/
元/ ![]() (
(![]() ,
, ![]() 为常数,且
为常数,且![]() ).
).

(1)写出易拉罐的制造费用![]() (元)关于
(元)关于![]() 的函数表达式,并求其定义域;
的函数表达式,并求其定义域;
(2)求易拉罐制造费用最低时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3+
x3+![]() x2+
x2+![]() x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
x(0<a<1,x∈R).若对于任意的三个实数x1,x2,x3∈[1,2],都有f(x1)+f(x2)>f(x3)恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com