
【题目】如图所示,已知椭圆:![]() (
(![]() )的离心率为
)的离心率为![]() ,右准线方程是直线l:
,右准线方程是直线l:![]() ,点P为直线l上的一个动点,过点P作椭圆的两条切线
,点P为直线l上的一个动点,过点P作椭圆的两条切线![]()
![]() ,切点分别为AB(点A在x轴上方,点B在x轴下方).
,切点分别为AB(点A在x轴上方,点B在x轴下方).
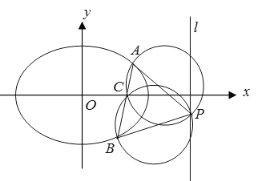
(1)求椭圆的标准方程;
(2)①求证:分别以![]()
![]() 为直径的两圆都恒过定点C;
为直径的两圆都恒过定点C;
②若![]() ,求直线
,求直线![]() 的方程.
的方程.
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
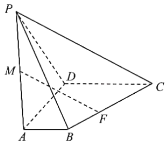
(I)求证:![]() ;
;
(II)求二面角_____的余弦值;
从①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.
这三个条件中任选一个,补充在上面问题中并作答.注:如果选择多个条件分别解答,按第一个解答计分.
(III)若![]() 是棱
是棱![]() 的中点,求证:对于棱
的中点,求证:对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() 为f(x)的导函数.
为f(x)的导函数.
(1)若a=b=c,f(4)=8,求a的值;
(2)若a≠b,b=c,且f(x)和![]() 的零点均在集合
的零点均在集合![]() 中,求f(x)的极小值;
中,求f(x)的极小值;
(3)若![]() ,且f(x)的极大值为M,求证:M≤
,且f(x)的极大值为M,求证:M≤![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥PABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD的中点,则
①棱AB与PD所在直线垂直;
②平面PBC与平面ABCD垂直;
③△PCD的面积大于△PAB的面积;
④直线AE与直线BF是异面直线.
以上结论正确的是________.(写出所有正确结论的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
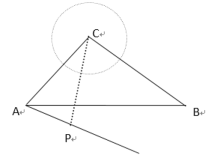
【题目】某工厂C发生爆炸出现毒气泄漏,已知毒气以圆形向外扩散,且半径以每分钟![]() 的速度增大. 一所学校A,位于工厂C南偏西
的速度增大. 一所学校A,位于工厂C南偏西![]() ,且与工厂相距
,且与工厂相距![]() .消防站B位于学校A的正东方向,且位于工厂C南偏东
.消防站B位于学校A的正东方向,且位于工厂C南偏东![]() ,立即以每分钟
,立即以每分钟![]() 的速度沿直线
的速度沿直线![]() 赶往工厂C救援,同时学校组织学生P从A处沿着南偏东
赶往工厂C救援,同时学校组织学生P从A处沿着南偏东![]() 的道路,以每分钟
的道路,以每分钟![]() 的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
的速度进行安全疏散(与爆炸的时间差忽略不计).要想在消防员赶往工厂的时间内(包括消防员到达工厂的时刻),保证学生的安全,学生撤离的速度应满足什么要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正整数,Sn为其前n项和,对于n=1,2,3,…,有
的各项均为正整数,Sn为其前n项和,对于n=1,2,3,…,有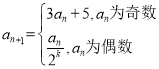 ,其中
,其中![]() 为使
为使![]() 为奇数的正整数,当
为奇数的正整数,当![]() 时,
时,![]() 的最小值为__________;当
的最小值为__________;当![]() 时,
时,![]() ___________.
___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通部门调查在高速公路上的平均车速情况,随机抽查了60名家庭轿车驾驶员,统计其中有40名男性驾驶员,其中平均车速超过![]() 的有30人,不超过
的有30人,不超过![]() 的有10人;在其余20名女性驾驶员中,平均车速超过
的有10人;在其余20名女性驾驶员中,平均车速超过![]() 的有5人,不超过
的有5人,不超过![]() 的有15人.
的有15人.
(1)完成下面的![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为,家庭轿车平均车速超过
的把握认为,家庭轿车平均车速超过![]() 与驾驶员的性别有关;
与驾驶员的性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶员 | |||
女性驾驶员 | |||
合计 |
(2)根据这些样本数据来估计总体,随机调查3辆家庭轿车,记这3辆车中,驾驶员为女性且平均车速不超过![]() 的人数为
的人数为![]() ,假定抽取的结果相互独立,求
,假定抽取的结果相互独立,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: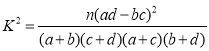
![]()
临界值表:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com