
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2017届甘肃省兰州市高三第一次诊断性考试数学(理)试卷(解析版) 题型:选择题
如图中的程序框图的算法思路来源于我国古代数学名著《九章算法》中的“更相减损术”,执行该程序框图,若输入 的值分别为
的值分别为 ,则输入的
,则输入的 ( )
( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届陕西省宝鸡市高三教学质量检测(一)数学(理)试卷(解析版) 题型:选择题
已知函数
的图象在点
处的切线为
,若
也与函数
, 
的图象相切,则
必满足( )
A. 
B. 
C. 
D. 
查看答案和解析>>
科目:高中数学 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:解答题
某厂有4台大型机器,在一个月中,一台机器至多出现1次故障,且每台机器是否出现故障是相互独立的,出现故障时需1名工人进行维修,每台机器出现故障需要维修的概率为 .
.
(1)若出现故障的机器台数为 ,求
,求 的分布列;
的分布列;
(2) 该厂至少有多少名工人才能保证每台机器在任何时刻同时出现故障时能及时进行维修的概率不少于90%?
(3)已知一名工人每月只有维修1台机器的能力,每月需支付给每位工人1万元的工资,每台机器不出现故障或出现故障能及时维修,就使该厂产生5万元的利润,否则将不产生利润,若该厂现有2名工人,求该厂每月获利的均值.
查看答案和解析>>
科目:高中数学 来源:2017届河南省洛阳市高三第二次统一考试(3月)数学(理)试卷(解析版) 题型:选择题
在 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为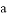 ,
, ,
, ,且
,且 ,则角
,则角 的最大值为( )
的最大值为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源:2017届河北省高三下学期二调考试数学(理)试卷(解析版) 题型:解答题
已知向量 ,
, ,设函数
,设函数 .
.
(1)若函数 的图象关于直线
的图象关于直线 对称,且
对称,且 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)在(1)的条件下,当 时,函数
时,函数 有且只有一个零点,求实数
有且只有一个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届贵州省贵阳市高三2月适应性考试(一)数学文试卷(解析版) 题型:解答题
选修4-5:不等式选讲
设
.
(1)若
恒成立,求实数
的取值范围;
(2)设
的最大值为
, 
均为正实数,当
时,求
的最小值.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年广东省揭阳市高二下学期第一次阶段考试数学(文)试卷(解析版) 题型:选择题
《张丘建算经》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有女不善织,日减功迟,初日织五尺,末日织一尺,今三十织迄,问织几何.”其意思为:有个女子不善于织布,每天比前一天少织同样多的布,第一天织五尺,最后一天织一尺,三十天织完,问三十天共织布( )
A.30尺 B.90尺 C.150尺 D.180尺
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com