考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线中的最值与范围问题
分析:(I)由题意,可得出),|PF1|+|PF2|=4>|F1F2|,根据椭圆的定义可知,点P的轨迹是椭圆,由此即可求出轨迹方程;
(II)由题意,可设出直线l的方程,由于其与圆C2相切,由相切关系可得出斜率k所满足的方程,再将直线方程与(I)中所求的轨迹方程联立,由弦长公式求出直线截曲线C1截得的线段的长的表达式,再根据所得表达式求其最值即可.
解答:
解:(Ⅰ)由F
1=(-1,0),F
2=(1,0),|PF
1|+|PF
2|=4>|F
1F
2|…(1分)
根据椭圆定义知P的轨迹为以F
1,F
2为焦点的椭圆,
其长轴2a=4,焦距2c=2,短半轴
b==,故C
1的方程为
+=1.…(4分)
(Ⅱ)设l:y=k(x+2),由过点A(-2,0)的直线l与曲线C
2相切得
=t(t+2),
化简得
t=,t∈(0,
](注:本处也可由几何意义求k与t的关系)…(6分)
由0<t=
<
,解得0≤k
2≤1…(7分)
联立
,消去y整理得(4k
2+3)x
2+16k
2x+16k
2-12=0,…(8分)
直线l被曲线C
1截得的线段一端点为A(-2,0),
设另一端点为B,解方程可得B(
,
),
所以|AB|=
=…(11分)
(注:本处也可由弦长公式结合韦达定理求得)
令
=n,则|AB|=
=,n∈(1,],
考查函数y=4n-
的性质知y=4n-
在区间(1,
]上是增函数,
所以n=
时,y=4n-
取最大值
,从而|AB|
min=
=.…(14分)
点评:本题考查定义法求轨迹方程,直线与圆相切的位置关系,弦长公式的应用,利用基本不等式求最值的方法,综合性强,运算量大,此类题的解答要注意方程思想的运用,转化与化归思想的运用



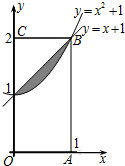 如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).随机往矩形OABC内投一点P,则点P落在区域M内的概率是( )
如图,在矩形OABC内:记抛物线y=x2+1与直线y=x+1围成的区域为M(图中阴影部分).随机往矩形OABC内投一点P,则点P落在区域M内的概率是( )