
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
分析 根据已知中函数的周期性和奇偶性,可得$f(\frac{7}{2})$=-$f(\frac{1}{2})$,进而得到答案.
解答 解:∵f(x)=f(x+2),
∴$f(\frac{7}{2})$=$f(\frac{3}{2})$=$f(-\frac{1}{2})$,
∵函数f(x)是定义在R上的奇函数,
∴$f(-\frac{1}{2})$=-$f(\frac{1}{2})$,
∵当x∈(0,1]时,f(x)=$\sqrt{x}$,
∴$f(\frac{1}{2})$=$\frac{\sqrt{2}}{2}$,
故$f(\frac{7}{2})$=-$\frac{\sqrt{2}}{2}$,
故选:D
点评 本题考查的知识点是函数的奇偶性,函数的周期性,是函数图象和性质的综合应用,难度中档.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | |
| B. | 若“p或q”为假命题,则“p且q”为真命题 | |
| C. | 命题“存在x0∈R,使得x${\;}_{0}^{2}$+x0+1<0”的否定是:“对任意x∈R,均有x2+x+1<0” | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆否命题为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
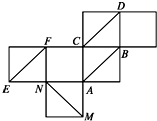
| A. | 点M到AB的距离为$\frac{{\sqrt{2}}}{2}$ | B. | AB与EF所成角是90° | ||
| C. | 三棱锥C-DNE的体积是$\frac{1}{6}$ | D. | EF与MC是异面直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 转速x/(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
| A. | 10转/s以下 | B. | 15转/s以下 | C. | 20转/s以下 | D. | 25转/s以下 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
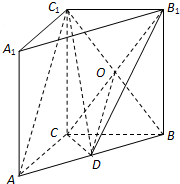 (理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.
(理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com