考点:数列的应用
专题:等差数列与等比数列
分析:本题(Ⅰ)利用多个直角三角形中的边角关系,求出边BPn与BPn+1 的关系,即an+1与an关系;(Ⅱ)利用已得的递推关系,构造新的等比数列,通过新数列的通项公式,得到数列{an}的通项公式,再对数列{an}分组求和,其中部分数列用错位相减法求和,得到本题的结论.
解答:
解:(Ⅰ)由题意:BP
n=a
n,BP
n+1=a
n+1,
则
BQn=BPncos60°=an,
QnC=3-an,
CRn=QnCcos60°=(3-an),
ARn=3-CRn=+an,
APn+1=ARncos60°=ARn=+an,
∴
BPn+1=3-APn+1=-an,
即
an+1=-an+ (n∈N*).
(Ⅱ)由即
an+1=-an+ (n∈N*),得到:
an+1-2=-(an-2),
∴{a
n-2}是以a
1-2=-1为首项,公比为
-的等比数列.
∴
an-2=-(-)n-1,即
an=2-(-)n-1 (n∈N*).
∴
nan=2n-n(-)n-1,则
Sn=2(1+2+3+…+n)-[1•(-)0+2•(-)1+…+n(-)n-1],
令
Tn=1•(-)0+2•(-)1+…+n(-)n-1,
-Tn=1•(-)1+2•(-)2+…+n•(-)n,
两式相减得:
Tn=1+(-)+(-)2+…+(-)n-1-n(-)n=
-n(-)n,
∴
Tn=.
∴
Sn=n(n+1)-.
点评:本题考查了解三角形、构造新数列、分组求和法、等差数列求和、错位相减法求和等知识点,本题的思维质量高,计算量较大,属于难题.

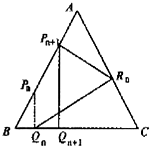 已知正△ABC的边长为3,P1是边AB上的一点且BP1=1,从P1向BC作垂线,垂足为Q1,从Q1向CA作垂线,垂足为R1,从R1向AB作垂线,垂足为P2.再从P2重复同样作法,依次得到点Q2,R2,P3,Q3,R3,…Pn,Qn,Rn,…,设BPn=an(n=1,2,3,…).
已知正△ABC的边长为3,P1是边AB上的一点且BP1=1,从P1向BC作垂线,垂足为Q1,从Q1向CA作垂线,垂足为R1,从R1向AB作垂线,垂足为P2.再从P2重复同样作法,依次得到点Q2,R2,P3,Q3,R3,…Pn,Qn,Rn,…,设BPn=an(n=1,2,3,…).

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 如图所示的电路图,设命题p:开关K闭合,命题q:开关K1闭合,命题s:开关K2闭合,命题t:开关K3闭合.
如图所示的电路图,设命题p:开关K闭合,命题q:开关K1闭合,命题s:开关K2闭合,命题t:开关K3闭合.