
| 自然状况 | 概率\盈利(元)\方案 | 订购40本 | 订购100本 | 订购120本 |
| 销售40本 | 0.2 | |||
| 销售100本 | 0.7 | |||
| 销售120本 | 0.1 |
分析 分别求出订购40,100,120(本)书的数学期望,比较即可得出结论.
解答 解:订购40本,销售40本时的盈利为(8-6)×40=80(元),因此,盈利数ξ的分布列为
| ξ | 80 | 80 | 80 |
| P | 0.2 | 0.7 | 0.1 |
| ξ | 20 | 200 | 200 |
| P | 0.2 | 0.7 | 0.1 |
| ξ | 0 | 180 | 240 |
| P | 0.2 | 0.7 | 0.1 |
点评 本题考查利用数学知识解决实际问题,考查数学期望,考查学生的计算能力,正确求出数学期望是关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
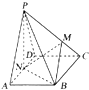 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.
如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),其中g′(x)是g(x)的导函数,则g′(3)=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com