
����Ŀ������Ϣʱ���Ľ��죬�����ֻ��ķ�չ�����š�Խ��Խ��Ϊ���ǽ�����һ�ַ�ʽ��ij�����ԡ�ʹ��
�Ž�������̬�Ƚ��е��飬�����ȡ��![]() �ˣ����������Ƶ���ֲ����� ��ʹ���Ž������ɵ�������
�ˣ����������Ƶ���ֲ����� ��ʹ���Ž������ɵ�������
�±�����ע�����䵥λ���꣩
���� |
|
|
|
|
|
|
Ƶ�� |
|
|
|
|
|
|
������ |
|
|
|
|
|
|
��1�������ԡ�����![]() ��Ϊ�ֽ�㡱��������ͳ��������������
��Ϊ�ֽ�㡱��������ͳ��������������![]() ����������ͨ�������ж��Ƿ��ڷ�����ĸ��ʲ�����
����������ͨ�������ж��Ƿ��ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ��ʹ���Ž�����̬�����˵������йء���
��ǰ������Ϊ��ʹ���Ž�����̬�����˵������йء���
���䲻���� | ������� | �ϼ� | |
�� | |||
���� | |||
�ϼ� |
��2��������������![]() ��
�� ![]() �ı��������и����ѡȡ���˽����ٵ��飬��ѡ�е�
�ı��������и����ѡȡ���˽����ٵ��飬��ѡ�е�![]() �����ɡ�ʹ���Ž�����������Ϊ�����������
�����ɡ�ʹ���Ž�����������Ϊ�����������![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
�����ο��������£�
|
|
|
|
|
|
|
|
|
|
�ο���ʽ��  ������
������![]() .
.
���𰸡�(1)�𰸼�������(2)�𰸼�����.
�����������������
(1)����������������������ɵ�![]() �������ڷ�����ĸ��ʲ�����
�������ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ��ʹ���Ž�����̬�����˵������йء�
��ǰ������Ϊ��ʹ���Ž�����̬�����˵������йء�
(2)����֪�� ![]() ���п���ȡֵΪ��
���п���ȡֵΪ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��������Ӧ�ĸ���ֵ��÷ֲ��У�Ȼ�����ɵ�
��������Ӧ�ĸ���ֵ��÷ֲ��У�Ȼ�����ɵ�![]() ����ѧ����Ϊ��
����ѧ����Ϊ�� ![]() .
.
���������
��1��![]() ��������
��������
���䲻���� | ������� | �ϼ� | |
�� |
|
|
|
���� |
|
| |
�ϼ� |
|
|
|
�ɱ��ɵã� ![]()
��![]()
�������ڷ�����ĸ��ʲ�����![]() ��ǰ������Ϊ��ʹ���Ž�����̬�����˵������йء�
��ǰ������Ϊ��ʹ���Ž�����̬�����˵������йء�
��2������֪�� ![]() ���п���ȡֵΪ��
���п���ȡֵΪ�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]()
�� ![]() ��
�� ![]() ��
��
![]() ��
�� ![]() .
.
����![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
| 0 | 1 | 2 | 3 |
|
|
|
|
|
����![]() ����ѧ����Ϊ��
����ѧ����Ϊ�� ![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
��1����![]() ʱ������
ʱ������![]() �ļ�ֵ��
�ļ�ֵ��
��2����![]() ��������
��������![]() ������
������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() Ϊ������e=2.71828������Ȼ�����ĵ�����������y=f��x���ڵ㣨1��f��1��������������x��ƽ�У� ������k��ֵ��
Ϊ������e=2.71828������Ȼ�����ĵ�����������y=f��x���ڵ㣨1��f��1��������������x��ƽ�У� ������k��ֵ��
������f��x���ĵ������䣻
������g��x��=��x2+x��f�䣨x��������f�䣨x��Ϊf��x���ĵ�������֤����������x��0��g��x����1+e��2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������һ��ֱ���õ�Բ�α�־�Բ��ΪC�������ĽӴ���ΪG����Բ�α�־����ͬһƽ���ڵĵ����ϵ�P����һ���۲�㣬��PG=50m���ڹ۲����ǰ��10m������PD=10m����һ����Ϊ10m����ED=10m���Ĺ������ס�����ߣ�����ڹ۲�����ܿ�����Բ�α�־����ּ�Ϊͼ�д�A��F��Բ���� 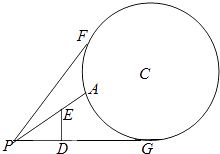
��1����Բ�α�־��뾶Ϊ25m����PG����ֱ��Ϊx�ᣬGΪ����ԭ�㣬����ֱ������ϵ����ԲC��ֱ��PF�ķ��̣�
��2�����ڵ�P���۲��Բ�α�־������ӽǣ�����APF��������ֵΪ ![]() �����Բ�α�־��İ뾶��
�����Բ�α�־��İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]()
��1����![]() ��
�� ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2����![]() ��
��![]() ����������ֵ��
����������ֵ��![]() .
.
��A����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��B����֤�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�� ![]() ��
��![]() ���е㣬����
���е㣬����![]() Ϊ���Σ�
���� ![]() ��
�� ![]() ��
�� ![]() ����ƽ��
����ƽ��![]() ƽ��
ƽ��![]() ��ƽ��
��ƽ��![]() ����
����![]() ���ڵ�
���ڵ�![]() ��ƽ��
��ƽ��![]() ��ƽ��
��ƽ��![]() ����ֱ��
����ֱ��![]() .
.
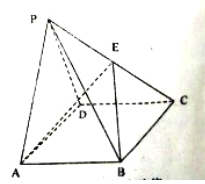
��1����֤�� ![]() ��
��
��2����![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ����
����![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ⳤ����ȵ��������ڽ���һ����ijѧ�������ĸ������ĵ�ƽ����������������õ�ͼ�Σ���ͼ��ʾ���� ��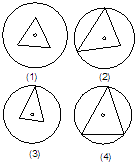
A.�����ĸ�ͼ�ζ�����ȷ��
B.ֻ�У�2����4������ȷ��
C.ֻ�У�4���Ǵ����
D.ֻ�У�1����2������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4-4������ϵ���������
�ڼ�����ϵ�У�����![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ���Լ���Ϊԭ�㣬����Ϊ
���Լ���Ϊԭ�㣬����Ϊ![]() ��������Ὠ��ƽ��ֱ������ϵ��ֱ��
��������Ὠ��ƽ��ֱ������ϵ��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������.
������.
��1��д������![]() �IJ������̺�ֱ��
�IJ������̺�ֱ��![]() ����ͨ���̣�
����ͨ���̣�
��2����֪��![]() ������
������![]() ��һ�㣬���
��һ�㣬���![]() ��ֱ��
��ֱ��![]() ����С����.
��������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com