
°æƒø°ø»ÁÕº£¨µÿ√Ê…œ”–“ª ˙÷±∑≈÷√µƒ‘≤–Œ±Í÷æŒÔ£¨‘≤–ƒŒ™C£¨”εÿ√ʵƒΩ”¥•µ„Œ™G£Æ”Α≤–Œ±Í÷æŒÔ‘⁄Õ¨“ª∆Ω√ʃ⁄µƒµÿ√Ê…œµ„P¥¶”–“ª∏ˆπ€≤‚µ„£¨«“PG=50m£Æ‘⁄π€≤‚µ„’˝«∞∑Ω10m¥¶£®º¥PD=10m£©”–“ª∏ˆ∏þŒ™10m£®º¥ED=10m£©µƒπ„∏Ê≈∆’⁄◊°¡À ”œþ£¨“Ú¥À‘⁄π€≤‚µ„À˘ƒÐø¥µΩµƒ‘≤–Œ±Í÷浃◊Ó¥Û≤ø∑÷º¥Œ™Õº÷–¥”AµΩFµƒ‘≤ª°£Æ 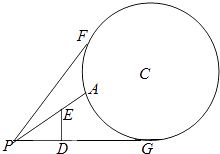
£®1£©»Ù‘≤–Œ±Í÷æŒÔ∞Îæ∂Œ™25m£¨“‘PGÀ˘‘⁄÷±œþŒ™x÷·£¨GŒ™◊¯±Í‘≠µ„£¨Ω®¡¢÷±Ω«◊¯±Íœµ£¨«Û‘≤C∫Õ÷±œþPFµƒ∑Ω≥ãª
£®2£©»Ù‘⁄µ„P¥¶π€≤‚∏√‘≤–Œ±Í÷浃◊Ó¥Û ”Ω«£®º¥°œAPF£©µƒ’˝«–÷µŒ™ ![]() £¨«Û∏√‘≤–Œ±Í÷æŒÔµƒ∞Îæ∂£Æ
£¨«Û∏√‘≤–Œ±Í÷æŒÔµƒ∞Îæ∂£Æ
°æ¥∞∏°ø
£®1£©Ω‚£∫‘≤C£∫x2+£®y©Å25£©2=252£Æ
÷±œþPB∑Ω≥ã∫x©Åy+50=0£Æ
…Ë÷±œþPF∑Ω≥ã∫y=k£®x+50£©£®k£æ0£©£¨
“ÚŒ™÷±œþPF”Α≤Cœý«–£¨À˘“‘ ![]() £¨Ω‚µ√
£¨Ω‚µ√ ![]()
À˘“‘÷±œþPF∑Ω≥ã∫ ![]() £¨º¥4x©Å3y+200=0
£¨º¥4x©Å3y+200=0
£®2£©Ω‚£∫…Ë÷±œþPF∑Ω≥ã∫y=k£®x+50£©£®k£æ0£©£¨‘≤C£∫x2+£®y©År£©2=r2£Æ
“ÚŒ™tan°œAPF=tan£®°œGPF©Å°œGPA£©= ![]() =
= ![]() £¨À˘“‘
£¨À˘“‘ ![]()
À˘“‘÷±œþPF∑Ω≥ã∫ ![]() £¨º¥40x©Å9y+2000=0£Æ
£¨º¥40x©Å9y+2000=0£Æ
“ÚŒ™÷±œþPF”Α≤Cœý«–£¨À˘“‘ ![]() £¨
£¨
ªØºÚµ√2r2+45r©Å5000=0£¨º¥£®2r+125£©£®r©Å40£©=0£Æ
π r=40
°æΩ‚Œˆ°ø£®1£©¿˚”√‘≤–ƒ”Î∞Îæ∂£¨ø…µ√‘≤µƒ∑Ω≥㨿˚”√PF”Α≤Cœý«–£¨ø…µ√÷±œþPFµƒ∑Ω≥㪣®2£©œ»«Û≥ˆ÷±œþPF∑Ω≥㨑Ÿ¿˚”√÷±œþPF”Α≤Cœý«–£¨«Û≥ˆ∏√‘≤–Œ±Í÷æŒÔµƒ∞Îæ∂£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∫Ø ˝f£®x£©=x3©Å3ax+b£®a£æ0£©µƒº´¥Û÷µŒ™6£¨º´–°÷µŒ™2£¨‘Úf£®x£©µƒºı«¯º‰ « £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝f£®x£©=ax3©Å6x2+1£¨»Ùf£®x£©¥Ê‘⁄Œ®“ªµƒ¡„µ„x0 £¨ «“x0£æ0£¨‘Úaµƒ»°÷µ∑∂Œß «£® £©
A.£®©Å°Þ£¨©Å4£©
B.£®4£¨+°Þ£©
C.£®©Å°Þ£¨©Å4 ![]() £©
£©
D.£®4 ![]() £¨+°Þ£©
£¨+°Þ£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø«Ûœ¬¡–πÿ”⁄xµƒ≤ªµ» ΩµƒΩ‚ºØ£∫
£®1£©©Åx2+7x£æ6£ª
£®2£©3x2+4x+2£æ0£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™ºØ∫œA={x|y= ![]() }£¨B={x|log2x°Ð1}£¨‘ÚA°…B=£® £©
}£¨B={x|log2x°Ð1}£¨‘ÚA°…B=£® £©
A.{x|©Å3°Ðx°Ð1}
B.{x|0£ºx°Ð1}
C.{x|©Å3°Ðx°Ð2}
D.{x|x°Ð2}
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬√Ê≥ÖÚøÚÕºµƒÀ„∑®Àº¬∑‘¥”⁄Œ“π˙π≈¥˙ ˝—ß√˚÷¯°∂æ≈’¬À„ ı°∑÷–µƒ°∞∏¸œýºıÀ ı°±£¨÷¥––∏√≥ÖÚøÚÕº£¨»Ù ‰»Îµƒ![]() ∑÷±Œ™14,18£¨‘Ú ‰≥ˆµƒ
∑÷±Œ™14,18£¨‘Ú ‰≥ˆµƒ![]() Œ™£® £©
Œ™£® £©

A. 0 B. 2 C. 4 D. 14
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄–≈œ¢ ±¥˙µƒΩÒÃÏ£¨ÀÊ◊≈ ÷ª˙µƒ∑¢’𣨰∞Œ¢–≈°±‘Ω¿¥‘Ω≥…Œ™»À√«Ωª¡˜µƒ“ª÷÷∑Ω Ω£¨ƒ≥ª˙ππ∂‘°∞ π”√Œ¢
–≈Ωª¡˜°±µƒÃ¨∂»Ω¯––µ˜≤È£¨Àʪ˙≥È»°¡À![]() »À£¨À˚√«ƒÍ¡‰µƒ∆µ ˝∑÷≤ºº∞∂‘ °∞ π”√Œ¢–≈Ωª¡˜°±‘Þ≥…µƒ»À ˝»Á
»À£¨À˚√«ƒÍ¡‰µƒ∆µ ˝∑÷≤ºº∞∂‘ °∞ π”√Œ¢–≈Ωª¡˜°±‘Þ≥…µƒ»À ˝»Á
œ¬±Ì£∫£®◊¢£∫ƒÍ¡‰µ•Œª£∫ÀÍ£©
ƒÍ¡‰ |
|
|
|
|
|
|
∆µ ˝ |
|
|
|
|
|
|
‘Þ≥…»À ˝ |
|
|
|
|
|
|
£®1£©£©»Ù“‘°∞ƒÍ¡‰![]() ÀÍŒ™∑÷ΩÁµ„°±£¨”…“‘…œÕ≥º∆ ˝æðÕÍ≥…œ¬√ʵƒ
ÀÍŒ™∑÷ΩÁµ„°±£¨”…“‘…œÕ≥º∆ ˝æðÕÍ≥…œ¬√ʵƒ![]() ¡–¡™±Ì£¨≤¢Õ®π˝º∆À„≈–∂œ «∑Ò‘⁄∑∏¥ÌŒÛµƒ∏≈¬ ≤ª≥¨π˝
¡–¡™±Ì£¨≤¢Õ®π˝º∆À„≈–∂œ «∑Ò‘⁄∑∏¥ÌŒÛµƒ∏≈¬ ≤ª≥¨π˝![]() µƒ«∞÷œ¬»œŒ™°∞ π”√Œ¢–≈Ωª¡˜µƒÃ¨∂»”λÀµƒƒÍ¡‰”–πÿ°±£ø
µƒ«∞÷œ¬»œŒ™°∞ π”√Œ¢–≈Ωª¡˜µƒÃ¨∂»”λÀµƒƒÍ¡‰”–πÿ°±£ø
ƒÍ¡‰≤ªµÕ”⁄ | ƒÍ¡‰µÕ”⁄ | ∫œº∆ | |
‘Þ≥… | |||
≤ª‘Þ≥… | |||
∫œº∆ |
£®2£©£©»Ù¥”ƒÍ¡‰‘⁄![]() £¨
£¨ ![]() µƒ±µ˜≤ȵƒ»À÷–∏˜Àʪ˙—°»°¡Ω»ÀΩ¯––◊∑◊Ÿµ˜≤È£¨º«—°÷–µƒ
µƒ±µ˜≤ȵƒ»À÷–∏˜Àʪ˙—°»°¡Ω»ÀΩ¯––◊∑◊Ÿµ˜≤È£¨º«—°÷–µƒ![]() »À÷–‘Þ≥…°∞ π”√Œ¢–≈Ωª¡˜°±µƒ»À ˝Œ™£¨«ÛÀʪ˙±‰¡ø
»À÷–‘Þ≥…°∞ π”√Œ¢–≈Ωª¡˜°±µƒ»À ˝Œ™£¨«ÛÀʪ˙±‰¡ø![]() µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚.
µƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚.
∏Ω£∫≤Œøº ˝æð»Áœ¬£∫
|
|
|
|
|
|
|
|
|
|
≤Œøºπ´ Ω£∫  £¨∆‰÷–
£¨∆‰÷–![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂Ø‘≤Mæ≠π˝µ„A£®3£¨0£©£¨«“”Î÷±œþl£∫x=©Å3œý«–£¨∂Ø‘≤‘≤–ƒMµƒπϺ£∑Ω≥ÃŒ™ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com