
【题目】已知动圆M经过点A(3,0),且与直线l:x=﹣3相切,动圆圆心M的轨迹方程为 .
【答案】y2=12x
【解析】解:法一:设动点M(x,y),设⊙M与直线l:x=﹣3的切点为N,则|MA|=|MN|,即动点M到定点A和定直线l:x=﹣3的距离相等,所以点M的轨迹是抛物线,且以A(3,0)为焦点,以直线l:x=﹣3为准线,
∴ ![]() =3,∴p=6.
=3,∴p=6.
∴圆心M的轨迹方程是y2=12x.
法二:设动点M(x,y),则点M的轨迹是集合P={M||MA|=|MN|},
即 ![]() ,化简,得y2=12x.
,化简,得y2=12x.
∴圆心M的轨迹方程为y2=12x
【考点精析】解答此题的关键在于理解抛物线的定义的相关知识,掌握平面内与一个定点![]() 和一条定直线
和一条定直线![]() 的距离相等的点的轨迹称为抛物线.定点
的距离相等的点的轨迹称为抛物线.定点![]() 称为抛物线的焦点,定直线
称为抛物线的焦点,定直线![]() 称为抛物线的准线.
称为抛物线的准线.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右顶点与右焦点的距离为
右顶点与右焦点的距离为![]() ,短轴长为
,短轴长为![]()
(I)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为![]() 求直线AB的方程。
求直线AB的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,地面上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高为10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧. 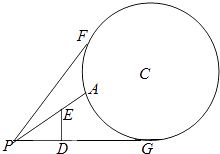
(1)若圆形标志物半径为25m,以PG所在直线为x轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即∠APF)的正切值为 ![]() ,求该圆形标志物的半径.
,求该圆形标志物的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中, ![]() 是
是![]() 的中点,底面
的中点,底面![]() 为矩形,
为矩形, ![]() ,
, ![]() ,
, ![]() ,且平面
,且平面![]() 平面
平面![]() ,平面
,平面![]() 与棱
与棱![]() 交于点
交于点![]() ,平面
,平面![]() 与平面
与平面![]() 交于直线
交于直线![]() .
.
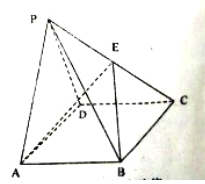
(1)求证: ![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长都相等的正三棱锥内接于一个球,某学生画出四个过球心的平面截球与正三棱锥所得的图形,如图所示,则( )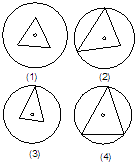
A.以上四个图形都是正确的
B.只有(2)(4)是正确的
C.只有(4)是错误的
D.只有(1)(2)是正确的
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)求与直线3x+4y-7=0垂直,且与原点的距离为6的直线方程;
(2)求经过直线l1:2x+3y-5=0与l2:7x+15y+1=0的交点,且平行于直线x+2y-3=0的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com