
为迎接6月6日的“全国爱眼日”,某高中学生会从全体学生中随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶),如图,若视力测试结果不低于5.0,则称为“好视力”.

(1)写出这组数据的众数和中位数;
(2)从这16人中随机选取3人,求至少有2人是“好视力”的概率;
(3)以这16人的样本数据来估计整个学校的总体数据,若从该校(人数很多)任选3人,记X表示抽到“好视力”学生的人数,求X的分布列及数学期望.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:选择题
已知(1+x)10=a0+a1(1-x)+a2(1-x)2+…+a10(1-x)10,则a8等于( )
A.180 B.90 C.-5 D.5
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:1-1集合的概念与运算(解析版) 题型:解答题
已知集合M={x|x(x-a-1)<0,x∈R},N={x|x2-2x-3≤0},若M∪N=N,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练2(解析版) 题型:填空题
在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2),定义:d(P,Q)=|x1-x2|+|y1-y2|.已知点B(1,0),点M为直线x-2y+2=0上的动点,则使d(B,M)取最小值时点M的坐标是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练1(解析版) 题型:填空题
对向量a=(a1,a2),b=(b1,b2)定义一种运算“?”:a?b=(a1,a2)?(b1,b2)=(a1b1,a2b2).已知动点P,Q分别在曲线y=sin x和y=f(x)上运动,且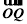 =m?
=m?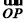 +n(其中O为坐标原点),若向量m=(
+n(其中O为坐标原点),若向量m=( ,3),n=(
,3),n=( ,0),则y=f(x)的最大值为________.
,0),则y=f(x)的最大值为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理配套特训:10-9离散型随机变量均值方差和正态分布(解析版) 题型:填空题
随机变量ξ的分布列如下
ξ | -1 | 0 | 1 |
P | a | b | c |
其中a,b,c成等差数列,若E(ξ)=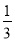 ,则D(ξ)=________.
,则D(ξ)=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理配套特训:10-9离散型随机变量均值方差和正态分布(解析版) 题型:选择题
已知随机变量X的分布列为
X | 1 | 2 | 3 |
P | 0.2 | 0.4 | 0.4 |
则E(6X+8)=( )
A.13.2 B.21.2 C.20.2 D.22.2
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:6-3二元一次不等式及简单的线性规划(解析版) 题型:解答题
为保增长、促发展,某地计划投资甲、乙两个项目,根据市场调研,知甲项目每投资100万元需要配套电能2万千瓦时,可提供就业岗位24个,GDP增长260万元;乙项目每投资100万元需要配套电能4万千瓦时,可提供就业岗位36个,GDP增长200万元.已知该地为甲、乙两个项目最多可投资3000万元,配套电能100万千瓦时,若要求两个项目能提供的就业岗位不少于840个,问如何安排甲、乙两个项目的投资额,才能使GDP增长的最多.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:3-1任意角弧度制及任意角的三角函数(解析版) 题型:选择题
给出下列命题:
①第二象限角大于第一象限角;
②三角形的内角是第一象限角或第二象限角;
③不论用角度制还是用弧度制度量一个角,它们与扇形所对半径的大小无关;
④若sinα=sinβ,则α与β的终边相同;
⑤若cosθ<0,则θ是第二或第三象限的角.
其中正确命题的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com