
【题目】已知向量 ![]() 、
、 ![]() 满足|
满足| ![]() |=1,|
|=1,| ![]() |=2,则|
|=2,则| ![]() +
+ ![]() |+|
|+| ![]() ﹣
﹣ ![]() |的最小值是 , 最大值是 .
|的最小值是 , 最大值是 .
【答案】4;![]()
【解析】解:记∠AOB=α,则0≤α≤π,如图,
由余弦定理可得:
| ![]() +
+ ![]() |=
|= ![]() ,
,
| ![]() ﹣
﹣ ![]() |=
|= ![]() ,
,
令x= ![]() ,y=
,y= ![]() ,
,
则x2+y2=10(x、y≥1),其图象为一段圆弧MN,如图,
令z=x+y,则y=﹣x+z,
则直线y=﹣x+z过M、N时z最小为zmin=1+3=3+1=4,
当直线y=﹣x+z与圆弧MN相切时z最大,
由平面几何知识易知zmax即为原点到切线的距离的 ![]() 倍,
倍,
也就是圆弧MN所在圆的半径的 ![]() 倍,
倍,
所以zmax= ![]() ×
× ![]() =
= ![]() .
.
综上所述,| ![]() +
+ ![]() |+|
|+| ![]() ﹣
﹣ ![]() |的最小值是4,最大值是
|的最小值是4,最大值是 ![]() .
.
所以答案是:4、 ![]() .
.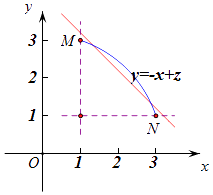
【考点精析】通过灵活运用函数的最值及其几何意义和余弦定理的定义,掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;余弦定理:![]() ;
;![]() ;
;![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1 , l2 , 直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )
A.16
B.14
C.12
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一袋中有大小相同的4个红球和2个白球,给出下列结论:
![]() 从中任取3球,恰有一个白球的概率是
从中任取3球,恰有一个白球的概率是![]() ;
;
![]() 从中有放回的取球6次,每次任取一球,则取到红球次数的方差为
从中有放回的取球6次,每次任取一球,则取到红球次数的方差为![]() ;
;
![]() 从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为
从中有放回的取球3次,每次任取一球,则至少有一次取到红球的概率为![]() .
.
其中所有正确结论的序号是______ .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1)B. C.
C. D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10 ![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(Ⅰ)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(Ⅱ)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.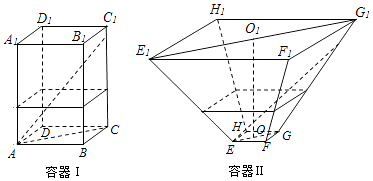
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某园林基地培育了一种新观赏植物,经过了一年的生长发育,技术人员从中抽取了部分植株的高度(单位:厘米)作为样本(样本容量为![]() )进行统计,按照[50,60),[60,70),[70,80),
)进行统计,按照[50,60),[60,70),[70,80),
[80,90),[90,100]分组做出频率分布直方图,并作出样本高度的茎叶图(图中仅列出了
高度在[50,60),[90,100]的数据).
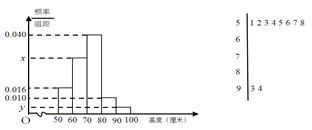
1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]()
2)在选取的样本中,从高度在80厘米以上(含80厘米)的植株中随机抽取3株,设随机变量![]() 表示所抽取的3株高度在 [80,90) 内的株数,求随机变量
表示所抽取的3株高度在 [80,90) 内的株数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人承揽一项业务,需做文字标牌4个,绘画标牌5个,现有两种规格的原料,甲种规格每张3m2,可做文字标牌1个,绘画标牌2个,乙种规格每张2m2,可做文字标牌2个,绘画标牌1个,求两种规格的原料各用多少张,才能使总的用料面积最小?

查看答案和解析>>
科目:高中数学 来源: 题型:
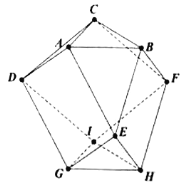
【题目】在如图所示的十一面体![]() 中,用
中,用![]() 种不同颜色给这个几何体各个顶点染色,每个顶点染一种颜色,要求每条棱的两端点异色,则不同的染色方案种数为__________.
种不同颜色给这个几何体各个顶点染色,每个顶点染一种颜色,要求每条棱的两端点异色,则不同的染色方案种数为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com