
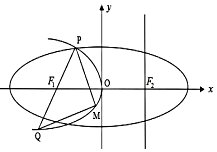
 如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.分析 (1)用m表示出a,b,根据基本不等式得出m的值,从而得出C1和C2的方程;
(2)用m表示出椭圆方程,联立方程组得出P点坐标,计算出△PF1F2的三边关于m的式子,从而确定m的值,求出PQ的距离和M到直线PQ的距离,利用二次函数性质得出△MPQ面积的最大值.
解答 解:(1)∵$c=m,e=\frac{c}{a}=\frac{1}{2}$,∴$a=2m,b=\sqrt{3}m$,
∴$\frac{a}{2}+\frac{{\sqrt{3}}}{b}$=m+$\frac{1}{m}$≥2,当且仅当m=$\frac{1}{m}$即m=1时取等号,
当m=1时,a=2,b=$\sqrt{3}$,
∴抛物线C1的方程为:y2=-4x,椭圆C2的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(2)因为$c=m,e=\frac{c}{a}=\frac{1}{2}$,则$a=2m,b=\sqrt{3}m$,
∴椭圆的标准方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{{3{m^2}}}=1$,设P(x0,y0),Q(x1,y1),
由$\left\{{\begin{array}{l}{\frac{x^2}{{4{m^2}}}+\frac{y^2}{{3{m^2}}}=1}\\{{y^2}=-4mx}\end{array}}\right.$得3x2-16mx-12m2=0,解得${x_0}=-\frac{2}{3}m$或x0=6m(舍去),
代入抛物线方程得${y_0}=\frac{{2\sqrt{6}}}{3}m$,即$P({-\frac{2m}{3},\frac{{2\sqrt{6}m}}{3}})$,
于是$|{P{F_1}}|=\frac{5m}{3},|{P{F_2}}|=2a-|{P{F_1}}|=\frac{7m}{3},|{{F_1}{F_2}}|=2m=\frac{6m}{3}$,
又△PF1F2的边长恰好是三个连续的自然数,∴m=3.
∴抛物线方程为y2=-12x,${F_1}({-3,0}),P({-2,2\sqrt{6}})$,
∴直线PQ的方程为$y=2\sqrt{6}({x+3})$.
联立$\left\{{\begin{array}{l}{y=2\sqrt{6}({x+3})}\\{{y^2}=-12x}\end{array}}\right.$,得${x_1}=-\frac{9}{2}$或x1=-2(舍去),于是$Q({-\frac{9}{2},-3\sqrt{6}})$.
∴$|{PQ}|=\sqrt{{{({-2+\frac{9}{2}})}^2}+{{({2\sqrt{6}+3\sqrt{6}})}^2}}=\frac{25}{2}$,
设$M({-\frac{t^2}{12},t})({t∈({-3\sqrt{6},2\sqrt{6}})})$到直线PQ的距离为d,则$d=\frac{{\sqrt{6}}}{30}×|{{{({t+\frac{{\sqrt{6}}}{2}})}^2}-\frac{75}{2}}|$,
∴当$t=-\frac{{\sqrt{6}}}{2}$时,${d_{max}}=\frac{{\sqrt{6}}}{30}×\frac{75}{2}=\frac{{5\sqrt{6}}}{4}$,
∴△MPQ的面积最大值为$\frac{1}{2}×\frac{25}{2}×\frac{{5\sqrt{6}}}{4}=\frac{{125\sqrt{6}}}{16}$.
此时M(-$\frac{1}{8}$,-$\frac{\sqrt{6}}{2}$),∴直线MP的方程为y=-$\frac{4\sqrt{6}}{3}$x-$\frac{2\sqrt{6}}{3}$.
点评 本题考查了圆锥曲线的性质,直线与圆锥曲线的位置关系,属于中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为$\frac{π}{3}$ | |
| B. | 函数f(x)的图象关于点$({\frac{7π}{9},0})$对称 | |
| C. | 函数f(x)在区间$({\frac{π}{4},\frac{11π}{24}})$上是增函数 | |
| D. | 由y=2cos2x的图象向右平移$\frac{5π}{12}$个单位长度可以得到函数f(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 分组 | 频数 | 频率 |
| [50,60) | 5 | 0.1 |
| [60,70) | m | 0.2 |
| [70,80) | 15 | n |
| [80,90) | 12 | 0.24 |
| 8 | 0.16 | |
| 合计 | 50 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com