
分析 由已知得|CQ|+|QM|=|CQ|+|QP|=|CP|=4,从而4=|CQ|+|QM|≥2$\sqrt{|\overrightarrow{CQ}|•|\overrightarrow{QM}}|$,问题得以解决
解答 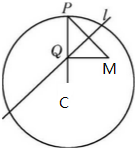 解:∵A是半径为4的圆C内一个定点,P是圆C上的一个动点,
解:∵A是半径为4的圆C内一个定点,P是圆C上的一个动点,
线段MP的垂直平分线l与半径CP相交于点Q,
∴|CQ|+|QM|=|CQ|+|QP|=|CP|=4,
∴4=|CQ|+|QM|≥2$\sqrt{|\overrightarrow{CQ}|•|\overrightarrow{QM}}|$,
∴|CQ|•|QM|≤4,
当且仅当Q为CP中点时取等号,
∴|CQ|•|QM|的最大值为4.
故答案为:4.
点评 本题考查两线段积的最大值的求法,是中档题,解题时要认真审题,注意圆形结合思想、均值定理的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (5,0),(-5,0) | B. | (0,5),(0,-5) | C. | (0,12),(0,-12) | D. | (12,0),(-12,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
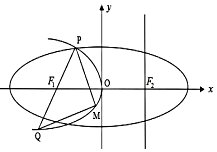 如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com