
| A. | 函数f(x)的最小正周期为$\frac{π}{3}$ | |
| B. | 函数f(x)的图象关于点$({\frac{7π}{9},0})$对称 | |
| C. | 函数f(x)在区间$({\frac{π}{4},\frac{11π}{24}})$上是增函数 | |
| D. | 由y=2cos2x的图象向右平移$\frac{5π}{12}$个单位长度可以得到函数f(x)的图象 |
分析 根据函数$f(0)=-\sqrt{3}$,求出φ,函数f(x)的图象关于直线$x=-\frac{π}{12}$对称,可得ω的值,求出了f(x)的解析式,依次对各选择判断即可.
解答 解:函数$f(x)=2sin({ωx+φ})({0<ω<12,|φ|<\frac{π}{2}})$,
∵$f(0)=-\sqrt{3}$,即2sinφ=$-\sqrt{3}$,
∵$-\frac{π}{2}<$φ$<\frac{π}{2}$
∴φ=$-\frac{π}{3}$
又∵函数f(x)的图象关于直线$x=-\frac{π}{12}$对称,
∴$-ω×\frac{π}{12}-\frac{π}{3}=\frac{π}{2}+kπ$,k∈Z.
可得ω=12k-10,
∵0<ω<12.
∴ω=2.
∴f(x)的解析式为:f(x)=2sin(2x-$\frac{π}{3}$).
最小正周期T=$\frac{2π}{2}=π$,∴A不对.
当x=$\frac{7π}{9}$时,可得y≠0,∴B不对.
令-$\frac{π}{2}≤$2x-$\frac{π}{3}$$≤\frac{π}{2}$,可得$-\frac{π}{12}≤x≤\frac{5π}{12}$,∴C不对.
函数y=2cos2x的图象向右平移$\frac{5π}{12}$个单位,可得2cos2(x-$\frac{5π}{12}$)=2cos(2x-$\frac{5π}{6}$)=2sin(2x-$\frac{5π}{6}+\frac{π}{2}$)=2sin(2x-$\frac{π}{3}$).∴D项正确.
故选D
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,确定f(x)的解析式是解决本题的关键.属于中档题.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (2,+∞] | C. | (0,2) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
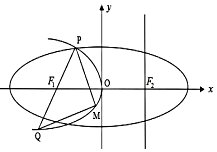 如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
如图,设抛物线C1:y2=-4mx(m>0)的准线l与x轴交于椭圆C2:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点F2,F1为C2的左焦点.椭圆的离心率为e=$\frac{1}{2}$,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{5}$ | B. | -$\frac{12}{5}$ | C. | $\frac{5}{12}$ | D. | -$\frac{5}{12}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com