
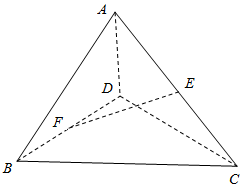
 空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小.
空间四边形ABCD中,AB=8.CD=6,E、F分别是对角线AC,BD的中点,且EF=6.求异面直线AB、CD所成的角的大小. 分析 可取AD的中点G,并连接FG,EG,根据条件便可得到FG∥AB,EG∥CD,并求得FG=4,EG=3,并且EF=6,这便得到∠FGE或其补角便为异面直线AB、CD所成的角,从而在△EFG中,由余弦定理可求出cos∠FGE,从而便可得出异面直线AB、CD所成的角的大小.
解答 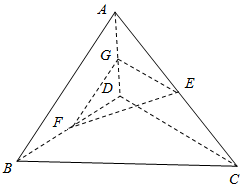 解:如图,取AD中点G,连接FG,EG,则:
解:如图,取AD中点G,连接FG,EG,则:
FG∥AB,EG∥CD,且$FG=\frac{1}{2}AB=4,EG=\frac{1}{2}CD=3$;
∴∠FGE或其补角为异面直线AB、CD所成的角;
在△EFG中,FG=4,EG=3,EF=6;
∴$cos∠FGE=\frac{F{G}^{2}+E{G}^{2}-E{F}^{2}}{2FG•EG}$=$\frac{16+9-36}{24}=-\frac{11}{24}$;
∴异面直线AB、CD所成的角的大小为$arccos\frac{11}{24}$.
点评 考查三角形中位线的性质,异面直线所成角的概念及求法,以及余弦定理,注意异面直线所成角的范围.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
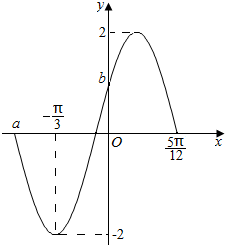 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,3x≤2x | B. | ?x∉R,3x<2x | C. | ?x0∈R,3x0≤2x0 | D. | ?x0∉R,3x0<2x0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com