
分析 根据题意,若S9>0,S10<0,由等差数列的性质分析可得a5>0,a6<0,进而可得等差数列{an}中有a1>a2>a3>a4>a5>0>a6>a7>a8>a9,则有0<$\frac{{2}^{1}}{{a}_{1}}$<$\frac{{2}^{2}}{{a}_{2}}$<$\frac{{2}^{3}}{{a}_{3}}$<$\frac{{2}^{4}}{{a}_{4}}$<$\frac{{2}^{5}}{{a}_{5}}$,当n≥6时,$\frac{{2}^{n}}{{a}_{n}}$<0,解可得答案.
解答 解:根据题意,等差数列{an}中,
若S9>0,则有S9=$\frac{({a}_{1}+{a}_{9})×9}{2}$=9a5>0,则有a5>0,
若S10<0,则有s10=$\frac{({a}_{1}+{a}_{10})}{2}$×10=(a5+a6)×5<0,则有a5+a6<0,
则有a5>0,a6<0,
则等差数列{an}为递减数列,则有a1>a2>a3>a4>a5>0>a6>a7>a8>a9,
则有数列{$\frac{{2}^{n}}{{a}_{n}}$}中,当n≤5时,有0<$\frac{{2}^{1}}{{a}_{1}}$<$\frac{{2}^{2}}{{a}_{2}}$<$\frac{{2}^{3}}{{a}_{3}}$<$\frac{{2}^{4}}{{a}_{4}}$<$\frac{{2}^{5}}{{a}_{5}}$,
当n≥6时,$\frac{{2}^{n}}{{a}_{n}}$<0,
故则$\frac{2}{a_1},\frac{2^2}{a_2},\frac{2^3}{a_3},…,\frac{2^9}{a_9}$中最大的是$\frac{{2}^{5}}{{a}_{5}}$,
故答案为:$\frac{{2}^{5}}{{a}_{5}}$.
点评 本题考查等差数列前n项和的性质,关键是分析得到数列{an}为递减数列.


科目:高中数学 来源: 题型:解答题
 在斜三棱柱ABC-A1B1C1中,顶点A1在底面ABC内的射影恰为线段AB的中点,AA1=2,△ABC为边长为2的正三角形,N为△ABC的中心,$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$.
在斜三棱柱ABC-A1B1C1中,顶点A1在底面ABC内的射影恰为线段AB的中点,AA1=2,△ABC为边长为2的正三角形,N为△ABC的中心,$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
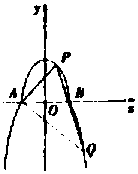 如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
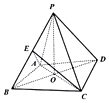 如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP中点,AC与BD交于点O,且OP⊥平面ABCD.
如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP中点,AC与BD交于点O,且OP⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com