
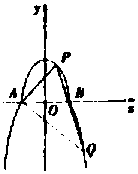
 ��ͼ������C���ϰ���Բ${C_1}��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��y��0��$�Ͳ���������${C_2}��y=-{x^2}+1��y��0��$���Ӷ��ɣ�C1��C2�Ĺ�����ΪA��B������C1��������Ϊ$\frac{{\sqrt{3}}}{2}$��
��ͼ������C���ϰ���Բ${C_1}��\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��y��0��$�Ͳ���������${C_2}��y=-{x^2}+1��y��0��$���Ӷ��ɣ�C1��C2�Ĺ�����ΪA��B������C1��������Ϊ$\frac{{\sqrt{3}}}{2}$������ ��1����C1��C2�ķ����У���y=0���ɵ�b=1����A��-1��0����B��1��0�����ϰ���ԲC1�����Ҷ��㣬��C1�İ뽹��Ϊc����$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$��a2-c2=b2-1���������a��
��2���ɣ�1�����ϰ���ԲC1�ķ���Ϊ$\frac{y^2}{4}+{x^2}=1��y��0��$��������֪��ֱ��l��x��غ�Ҳ����ֱ�����䷽��Ϊ
y=k��x-1����k��0��������C1�ķ��̣������ã�k2+4��x2-2k2x+k2-4=0�����P������Ϊ��xP��yP�����������ʽ���õ�P������Ϊ$��\frac{{{k^2}-4}}{{{k^2}+4}}��\frac{-8k}{{{k^2}+4}}��$��ͬ������$\left\{\begin{array}{l}{y=k��x-1����k��0}\\{y=-{x}^{2}+1��y��0}\end{array}\right.$���õ�Q������Ϊ��-k-1��-k2-2k�����������֪AP��AQ������$\overrightarrow{A{P_1}}•\overrightarrow{AQ}=0$�����ɵó�k��
��� �⣺��1����C1��C2�ķ����У���y=0���ɵ�b=1����A��-1��0����B��1��0�����ϰ���ԲC1�����Ҷ��㣬
��C1�İ뽹��Ϊc����$\frac{c}{a}=\frac{{\sqrt{3}}}{2}$��a2-c2=b2-1��
�ɵ�a=2������a=2��b=1��
��2���ɣ�1�����ϰ���ԲC1�ķ���Ϊ$\frac{y^2}{4}+{x^2}=1��y��0��$��
������֪��ֱ��l��x��غ�Ҳ����ֱ�����䷽��Ϊy=k��x-1����k��0����
����C1�ķ��̣������ã�k2+4��x2-2k2x+k2-4=0��
���P��������xP��yP����
��Ϊֱ��l����B������x=1�Ƿ��̵�һ������
�������ʽ����${x_P}=\frac{{{k^2}-4}}{{{k^2}+4}}��{y_P}=\frac{-8k}{{{k^2}+4}}$�����Ե�P������Ϊ$��\frac{{{k^2}-4}}{{{k^2}+4}}��\frac{-8k}{{{k^2}+4}}��$��
ͬ������$\left\{\begin{array}{l}{y=k��x-1����k��0}\\{y=-{x}^{2}+1��y��0}\end{array}\right.$���õ�Q������Ϊ��-k-1��-k2-2k����
����$\overrightarrow{AP}=��\frac{{2{k^2}}}{{{k^2}+4}}��\frac{{-8{k^2}}}{{{k^2}+4}}����\overrightarrow{AQ}=��-k��-{k^2}+2k��$��
�������֪AP��AQ������$\overrightarrow{A{P_1}}•\overrightarrow{AQ}=0$����$\frac{{2{k^2}}}{{{k^2}+4}}•��-k��+\frac{{-8{k^2}}}{{{k^2}+4}}•��-{k^2}-2k��=0$��
��$\frac{{-2{k^2}}}{{{k^2}+4}}[k-4��k+2��]=0$��
��Ϊk��0������k-4��k+2��=0�����$k=-\frac{8}{3}$��
�����飬$k=-\frac{8}{3}$�������⣬��ֱ��l�ķ���Ϊ$y=-\frac{8}{3}��x-1��$��
���� ���⿼����ֱ������Բ�������ཻ���⡢һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��Բ�����ʡ�������ֱ���������Ĺ�ϵ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{5}{3}$ | B�� | -$\frac{1}{3}$ | C�� | -1 | D�� | -5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
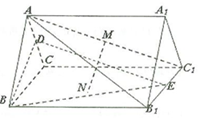 ��ͼ����������ABC-A1B1C1�У�����$A{A_1}=\sqrt{3}$��AB=2��D��E�ֱ�Ϊ��AC��B1C1���е㣬M��N�ֱ�Ϊ�߶�AC1��BE���е㣮
��ͼ����������ABC-A1B1C1�У�����$A{A_1}=\sqrt{3}$��AB=2��D��E�ֱ�Ϊ��AC��B1C1���е㣬M��N�ֱ�Ϊ�߶�AC1��BE���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
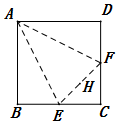 ��ͼ����������ABCD�У�E��F�ֱ�ΪBC��CD���е㣬HΪEF���е㣬��AE��EF��FA������������ʹB��C��D�غ��ڵ�O�����������壬����������A-OEF�У�����˵������ȷ������Ǣڣ�
��ͼ����������ABCD�У�E��F�ֱ�ΪBC��CD���е㣬HΪEF���е㣬��AE��EF��FA������������ʹB��C��D�غ��ڵ�O�����������壬����������A-OEF�У�����˵������ȷ������Ǣڣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�4�� | B�� | ��4��+�ޣ� | C�� | ��-�ޣ�2�� | D�� | ��2��+�ޣ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com