
分析 m=${∫}_{-1}^{1}$(6x2+tanx)dx=$(2{x}^{3}){|}_{-1}^{1}$+${∫}_{-1}^{1}tanxdx$=4,可得$(2x+\sqrt{3})^{4}$=a0+a1x+a2x2+…+${a}_{4}{x}^{4}$,分别令x=1,x=-1,即可得出.
解答 解:m=${∫}_{-1}^{1}$(6x2+tanx)dx=$(2{x}^{3}){|}_{-1}^{1}$+${∫}_{-1}^{1}tanxdx$=4,
∴$(2x+\sqrt{3})^{4}$=a0+a1x+a2x2+…+${a}_{4}{x}^{4}$,
令x=1,则a0+a1+a2+a3+a4=$(2+\sqrt{3})^{4}$,
令x=-1,则a0-a1+a2-a3+a4=$(2-\sqrt{3})^{4}$,
则(a0+a2+a4)2-(a1+a3)2=(a0+a1+a2+a3+a4)(a0-a1+a2-a3+a4)=$(2+\sqrt{3})^{4}$$(2-\sqrt{3})^{4}$=1.
故答案为:1.
点评 本题考查了微积分基本定理、二项式定理的应用,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 24 | C. | 8 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (1,2] | C. | (1,3] | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
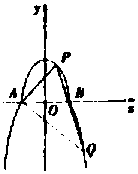 如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{5}}{2}$-1 | B. | $\frac{3\sqrt{3}}{2}$-1 | C. | 2$\sqrt{3}$-1 | D. | $\sqrt{10}$-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com