
分析 ①设函数s(t)表示此人第一天距离A地的路程,则其是一个不减的函数,设函数l(t)表示此人第二天距离A地的路程,则其是一个不增的函数,画出函数的大致图象,由图可知①正确;
②画出两天的速度(自变量为时间t)函数图象并求定积分(即与x轴围城的面积),由定积分相等可知两函数在(0,6)内必有交点可知②正确;
③结合题意举例说明错误.
解答 解:①、设函数s(t)表示此人第一天距离A地的路程,则其是一个不减的函数,设函数l(t)表示此人第二天距离A地的路程,则其是一个不增的函数,其中t表示时间,s(t)、l(t)的定义域都是[0,6],值域相同.同一坐标系画出s(t)、l(t)的图象,必有一个交点,即两天中在此刻经过此点(如图1),故①正确;
②、画出两天的速度(自变量为时间t)函数图象并求定积分(即与x轴围城的面积),其几何意义就是路程,不可能一个总在另一个下方.在交点处时刻,他们的速度相等(如图2),故②正确;
③、在某个路程函数s(t)中,过s(t) 上一点作平行于t,s轴的矩形,如果四个顶点都在曲线上,则意味着速度的绝对值相等,(对角线就是割线,斜率就是平均速度),但不是每种函数曲线都能成功,图3 显示可以,函数模型就是两个一次函数,图4显示不成功,可以构造函数模型为(这里假定时间t∈(0,6)AB之间距离为4)$s(x)=\left\{\begin{array}{l}\frac{1}{2}x,x∈(0,2)\\ \frac{3}{4}x-\frac{1}{2},x∈[2,6)\end{array}\right.$,$l(x)=\left\{\begin{array}{l}-3x+4,x∈(0,1)\\-\frac{1}{5}(x-6),x∈[1,6)\end{array}\right.$.在这个图象上经计算,找不到这样的矩形,故③错误.
∴正确的说法是①②.
故答案为:①②.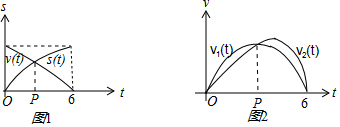
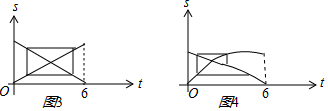
点评 本题考查函数的图象,贴近生活,叙述简单,考察学生运用数学知识分析问题解决问题的能力,运用了数学建模思想,函数与方程思想,数形结合思想,对具体问题进行抽象思维,是中档题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{π-2}{4π}$ | C. | $\frac{1}{2π}$ | D. | $\frac{3π+2}{4π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | $[\frac{1}{8},+∞)$ | C. | $[-1,\frac{1}{8}]$ | D. | $[\frac{1}{8},1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=3sin($\frac{π}{6}$-2x) | B. | f(x)=3sin(2x-$\frac{π}{6}$) | C. | f(x)=3sin($\frac{π}{3}$-2x) | D. | f(x)=3sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com