
分析 ①根据正弦函数的单调性和特殊角的三角函数值判断a<$\frac{{\sqrt{2}}}{2}$;
②根据同角的三角函数关系与两角和的正弦公式求出sin73°的值.
解答 解:①sin43°=a,且sin43°<sin45°=$\frac{\sqrt{2}}{2}$,
∴a<$\frac{{\sqrt{2}}}{2}$;
②又cos43°=$\sqrt{1{-sin}^{2}43°}$=$\sqrt{1{-a}^{2}}$,
∴sin73°=sin(43°+30°)
=sin43°cos30°+cos43°sin30°
=$\frac{\sqrt{3}}{2}$a+$\frac{\sqrt{1{-a}^{2}}}{2}$
=$\frac{\sqrt{3}a+\sqrt{1{-a}^{2}}}{2}$.
故答案为:<,$\frac{{\sqrt{3}a+\sqrt{1-{a^2}}}}{2}$.
点评 本题考查了三角恒等变换与同角的三角函数关系应用问题,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3-\sqrt{6}}{6}$,$\frac{3+\sqrt{6}}{6}$] | B. | [$\frac{3-\sqrt{6}}{6}$,1] | C. | [$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{6}$,$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{3}}{6}$] | D. | [$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{3}}{6}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
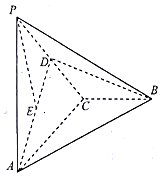 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{181}{16}$ | B. | 1 | C. | $\frac{9}{13}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在斜三棱柱ABC-A1B1C1中,顶点A1在底面ABC内的射影恰为线段AB的中点,AA1=2,△ABC为边长为2的正三角形,N为△ABC的中心,$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$.
在斜三棱柱ABC-A1B1C1中,顶点A1在底面ABC内的射影恰为线段AB的中点,AA1=2,△ABC为边长为2的正三角形,N为△ABC的中心,$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com