
分析 (1)对x的范围进行讨论,去绝对值符号解出;
(2)利用基本不等式证明.
解答 (1)解:当x<1时,不等式化为1-x+2-x-3>0,解得x<0;
当1≤x≤2时,不等式化为x-1+2-x-3>0,方程无解;
当x>2,不等式化为x-1+x-2-3>0,解得x>3.
综上,不等式的解集为{x|x<0或x>3}.
(2)证明:∵a1,a2,…,an∈R,
∴1+a1≥2$\sqrt{{a}_{1}}$,1+a2≥2$\sqrt{{a}_{2}}$,…,1+an≥2$\sqrt{{a}_{n}}$,
∴(1+a1)•(1+a2)…(1+an)≥2n•$\sqrt{{a}_{1}{a}_{2}…{a}_{n}}$=2n.
当且仅当a1=a2=…=an=1时取等号.
点评 本题考查了含绝对值的不等式的解法,基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 如果不买彩票,那么就不能中奖,因为你买了彩票,所以你一定中奖 | |
| B. | 因为a>b,a>c,所以a-b>a-c | |
| C. | 若a,b均为正实数,则lg a+lg b≥$\sqrt{lga•lgb}$ | |
| D. | 若a为正实数,ab<0,则$\frac{a}{b}$+$\frac{b}{a}$=-($\frac{-a}{b}$+$\frac{-b}{a}$)≤-2 $\sqrt{(\frac{-a}{b})•(\frac{-b}{a})}$=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 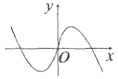 | B. | 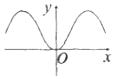 | C. | 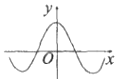 | D. | 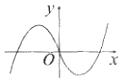 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{π-2}{4π}$ | C. | $\frac{1}{2π}$ | D. | $\frac{3π+2}{4π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com