
分析 根据条件求出命题p,q为真命题的等价条件,结合复合命题真假关系进行求解即可.
解答 解:命题p:关于x的方程x2-ax+4=0有实根,则△=a2-16≥0,解得a≥4,或a≤-4.
命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,∴$-\frac{a}{4}≤3$,解得a≥-12.
若p∧q是真命题,
则p,q同时为真命题,
则$\left\{\begin{array}{l}{a≥4或a≤-4}\\{a≥-12}\end{array}\right.$,
即-12≤a≤-4或a≥4,
故答案为:[-12,-4]∪[4,+∞)
点评 本题考查了复合命题真假的判定方法、函数的性质、一元二次的实数根与判别式的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
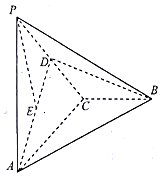 如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为PC的中点,E为AD的中点,PA=AC=2,BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{181}{16}$ | B. | 1 | C. | $\frac{9}{13}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{7}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在斜三棱柱ABC-A1B1C1中,顶点A1在底面ABC内的射影恰为线段AB的中点,AA1=2,△ABC为边长为2的正三角形,N为△ABC的中心,$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$.
在斜三棱柱ABC-A1B1C1中,顶点A1在底面ABC内的射影恰为线段AB的中点,AA1=2,△ABC为边长为2的正三角形,N为△ABC的中心,$\overrightarrow{{C}_{1}M}$=2$\overrightarrow{MB}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
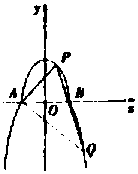 如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com