
| A. | (-∞,4) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
分析 求函数f(x)的定义域,求出f′(x),利用导数和极值之间的关系将条件转化:f′(x)=0在(0,+∞)上有根,即即2x2-ax+1=0在(0,+∞)上有根,根据二次方程根的分布问题列出方程组,根据条件列出关于a的不等式,求出a的范围.
解答 解:f(x)=ax-x2-lnx,x∈(0,+∞),
则f′(x)=a-2x-$\frac{1}{x}$=-$\frac{2{x}^{2}-ax+1}{x}$,
∵函数f(x)存在极值,∴f′(x)=0在(0,+∞)上有根,
即2x2-ax+1=0在(0,+∞)上有根,∴△=a2-8≥0,
显然当△=0时,F(x)无极值,不合题意;
∴方程必有两个不等正根,记方程2x2-ax+1=0的两根为x1,x2,x1+x2=$\frac{a}{2}$,x1x2=$\frac{1}{2}$,
f(x1),f(x2)是函数F(x)的两个极值,
由题意得,f(x1)+f(x2)=a(x1+x2)-(x12+x22)-(lnx1+lnx2)
=$\frac{{a}^{2}}{2}$-$\frac{{a}^{2}}{4}$+1-ln$\frac{1}{2}$>5-ln$\frac{1}{2}$,
化简解得,a2>16,满足△>0,
又x1+x2=$\frac{a}{2}$>0,即a>0,
∴∴a的取值范围是(4,+∞),
故选:B.
点评 本题考查导数与函数的单调性、极值的关系,以及二次方程根的分布问题,考查转化思想,化简、变形能力,综合性大、难度大,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
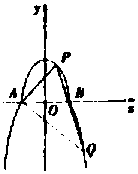 如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.
如图,曲线C由上半椭圆${C_1}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0,y≥0)$和部分抛物线${C_2}:y=-{x^2}+1(y≤0)$连接而成,C1与C2的公共点为A,B,其中C1的离心率为$\frac{{\sqrt{3}}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
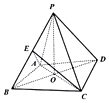 如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP中点,AC与BD交于点O,且OP⊥平面ABCD.
如图,在四棱锥P-ABCD中,∠BAD=120°,AB=AD=2,△BCD是等边三角形,E是BP中点,AC与BD交于点O,且OP⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{5}}{2}$-1 | B. | $\frac{3\sqrt{3}}{2}$-1 | C. | 2$\sqrt{3}$-1 | D. | $\sqrt{10}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com