
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)若对任意的![]() ,
,![]() ,都有
,都有![]() 恒成立,试求m的取值范围;
恒成立,试求m的取值范围;
(2)用![]() 表示m,n中的最小值,设函数
表示m,n中的最小值,设函数![]() (
(![]() ),讨论关于x的方程
),讨论关于x的方程![]() 的实数解的个数.
的实数解的个数.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据![]() 恒成立转化为
恒成立转化为![]() 恒成立,即来研究函数
恒成立,即来研究函数![]() 的最值,再分当
的最值,再分当![]() ,
,![]() ,
,![]() 时三种情况分分类讨论求解.
时三种情况分分类讨论求解.
(2) 将方程![]() 的实数解的个数,转化为函数
的实数解的个数,转化为函数![]() 零点的个数问题来研究,根据函数
零点的个数问题来研究,根据函数![]() 的定义,分
的定义,分![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() 三种情况下,对
三种情况下,对![]() 讨论.
讨论.
(1)![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
所以![]() ,
,
解得![]() ,不合题意舍去,
,不合题意舍去,
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,![]() ,
,
而![]() ,
,![]() ,
,
所以有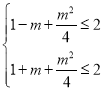 ,
,
解得![]() ,即
,即![]() ,
,
当![]() 即
即![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() ,
,
![]() ,
,
解得![]() ,不合题意,
,不合题意,
.综上所述,m的取值范围为![]() .
.
(2)方程![]() 的实数解的个数
的实数解的个数![]() 函数
函数![]() 零点的个数.
零点的个数.
①当![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以函数![]() 在
在![]() 上没有零点,即方程
上没有零点,即方程![]() 在
在![]() 上没有实数解;
上没有实数解;
②当![]() 时,
时,![]() ,
,![]() ,
,
若![]() ,即
,即![]() 时,
时,
![]() ,所以
,所以![]() 是函数
是函数![]() 的零点,
的零点,
即方程![]() 有一实数解
有一实数解![]() ,
,
若![]() ,即
,即![]() ,
,
![]() ,所以
,所以![]() 此时不是函数
此时不是函数![]() 的零点,
的零点,
即方程![]() 此时无实数解;
此时无实数解;
.③当![]() 时,
时,![]() ,所以只需考虑
,所以只需考虑![]() 在
在![]() 上的零点个数,
上的零点个数,
则由![]() 得
得![]() ,
,![]() 即问题等价于直线
即问题等价于直线![]() 与函数
与函数![]() ,
,![]() 图象的交点的个数.
图象的交点的个数.
由于对勾函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
结合![]() ,
,![]() 的图象可知,
的图象可知,
当![]() 时,
时,![]() 与函数
与函数![]() ,
,![]() 的图象没有交点,
的图象没有交点,
即函数![]() 在
在![]() 上没有零点,即方程
上没有零点,即方程![]() 在
在![]() 上没有实数解;
上没有实数解;
当![]() 或
或![]() 时,
时,![]() 在
在![]() 上有一个实数解;
上有一个实数解;
当![]() 时,
时,![]() 在
在![]() 上有两个实数解;
上有两个实数解;
综上所述,当![]() 或
或![]() 时,方程
时,方程![]() 有一个实数解,
有一个实数解,
当![]() 或
或![]() 时,方程
时,方程![]() 在
在![]() 上有两个实数解,
上有两个实数解,
当![]() 时,方程
时,方程![]() 在
在![]() 上有三个实数解.
上有三个实数解.


科目:高中数学 来源: 题型:
【题目】某中学的高二(1)班男同学有45名,女同学有15名,老师按照分层抽样的方法组建了一个4人的课外兴趣小组.
(1)求课外兴趣小组中男、女同学的人数;
(2)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出1名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(3)试验结束后,第一次做试验的同学得到的试验数据为68,70,71,72,74,第二次做试验的同学得到的试验数据为69,70,70,72,74 ,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“双十一”期间,某淘宝店主对其商品的上架时间![]() (小时)和销售量
(小时)和销售量![]() (件)的关系作了统计,得到了如下数据并研究.
(件)的关系作了统计,得到了如下数据并研究.
上架时间 | 2 | 4 | 6 | 8 | 10 | 12 |
销售量 | 64 | 138 | 205 | 285 | 360 | 430 |
(1)求表中销售量![]() 的平均数和中位数;
的平均数和中位数;
(2)① 作出散点图,并判断变量![]() 与
与![]() 是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程
是否线性相关?若研究的方案是先根据前5组数据求线性回归方程,再利用第6组数据进行检验,求线性回归方程![]() ;
;
②若根据①中线性回归方程得到商品上架12小时的销售量的预测值与检测值不超过3件,则认为得到的线性回归方程是理想的,试问:①中的线性回归方程是否理想.
附:线性回归方程![]() 中,
中, 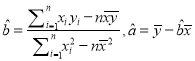 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护环境,某工厂在政府部门的支持下,进行技术改进:把二氧化碳转化为某种化工产品,经测算,该处理成本y(万元)与处理量x(吨)之间的函数关系可近似地表示为: ,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
,且每处理一吨二氧化碳可得价值为20万元的某种化工产品.
(1)当![]() 时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
时,判断该技术改进能否获利?如果能获利,求出最大利润;如果不能获利,则国家至少需要补贴多少万元,该工厂才不亏损?
(2)当处理量为多少吨时,每吨的平均处理成本最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题![]() 对任意实数
对任意实数![]() ,不等式
,不等式![]() 恒成立;命题
恒成立;命题![]() 方程
方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线.
轴上的双曲线.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若命题:“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”
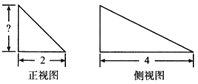
中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”![]() 现有一阳马,其正视图和侧视图是如图所示的直角三角形
现有一阳马,其正视图和侧视图是如图所示的直角三角形![]() 若该阳马的顶点都在同一个球面上,且该球的表面积为
若该阳马的顶点都在同一个球面上,且该球的表面积为![]() ,则该“阳马”的体积为__.
,则该“阳马”的体积为__.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是两个小区所在地,
是两个小区所在地,![]() 、
、![]() 到一条公路
到一条公路![]() 的垂直距离分别为
的垂直距离分别为![]()
![]() ,
,![]()
![]() ,
,![]() 两端之间的距离为
两端之间的距离为![]()
![]() .
.
(1)某移动公司将在![]() 之间找一点
之间找一点![]() ,在
,在![]() 处建造一个信号塔,使得
处建造一个信号塔,使得![]() 对
对![]() 、
、![]() 的张角与
的张角与![]() 对
对![]() 、
、![]() 的张角相等,试确定点
的张角相等,试确定点![]() 的位置.
的位置.
(2)环保部门将在![]() 之间找一点
之间找一点![]() ,在
,在![]() 处建造一个垃圾处理厂,使得
处建造一个垃圾处理厂,使得![]() 对
对![]() 、
、![]() 所张角最大,试确定点
所张角最大,试确定点![]() 的位置.
的位置.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com