
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为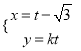 (
(![]() 为参数),直线
为参数),直线![]() 的参数程为
的参数程为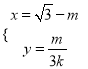 (
(![]() 为参数),设直线
为参数),设直线![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时点
变化时点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求出曲线![]() 的普通方程;
的普通方程;
(2)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为曲线
为曲线![]() 的动点,求点
的动点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象过点
的图象过点![]() ,图象与P点最近的一个最高点坐标为
,图象与P点最近的一个最高点坐标为![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() ,求函数
,求函数![]() 的值域;
的值域;
(3)若方程![]() 在
在![]() 上有两个不相等的实数根
上有两个不相等的实数根![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,{bn}是各项均为正数的等比数列,且b1=a1=1,b3=a4,b1+b2+b3=a3+a4.
(1)求数列{an},{bn}的通项公式;
(2)设cn=anbn,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求适合下列条件的双曲线的标准方程:
(1)过点(3,-![]() ),离心率e=
),离心率e=![]() ;
;
(2)中心在原点,焦点F1,F2在坐标轴上,实轴长和虚轴长相等,且过点P(4,-![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() ,顶点
,顶点![]() 在底面
在底面![]() 上的射影恰为点
上的射影恰为点![]() ,且
,且![]()

(1)证明:平面![]()
![]() 平面
平面![]() ;
;
(2)求棱![]() 与
与![]() 所成的角的大小;
所成的角的大小;
(3)若点![]() 为
为![]() 的中点,并求出二面角
的中点,并求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P是抛物线y2=4x上的一个动点,F为抛物线的焦点,记点P到点A(-1,1)的距离与点P到直线x= - 1的距离之和的最小值为M,若B(3,2),记|PB|+|PF|的最小值为N,则M+N= ______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届河南省南阳市第一中学高三上学期第八次考试】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于60分到140分之间(满分150分),将统计结果按如下方式分成八组:第一组[60,70),第二组[70,80),……,第八组:[130,140],如图是按上述分组方法得到的频率分布直方图的一部分.
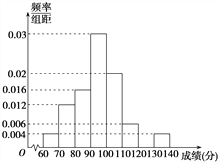
(1)求第七组的频率,并完成频率分布直方图;
(2)估计该校的2000名学生这次考试成绩的平均分(可用中值代替各组数据平均值);
(3)若从样本成绩属于第一组和第六组的所有学生中随机抽取2名,求他们的分差小于10分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com