
分析 (1)x0f(x0)≥g(x0)可化为$a≤{x_0}^2-2ln{x_0}$,
构造h(x)=x2-2lnx,求出其值域即可.
(2)$\frac{{H({x_1})-H({x_2})}}{{{x_1}-{x_2}}}=\frac{2}{{{x_1}-{x_2}}}ln\frac{{{x_1}+1}}{{{x_2}+1}}+({x_1}+{x_2})$;$H'(\frac{{{x_1}+{x_2}}}{2})=\frac{4}{{{x_1}+{x_2}+2}}+({x_1}+{x_2})$;
故可化为$\frac{2}{{{x_1}-{x_2}}}ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{4}{{{x_1}+{x_2}+2}}$,即$ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{{2({x_1}-{x_2})}}{{{x_1}+{x_2}+2}}$
又即$ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{{2[({x_1}+1)-({x_2}+1)]}}{{({x_1}+1)+({x_2}+1)}}=\frac{{2[\frac{{{x_1}+1}}{{{x_2}+1}}-1]}}{{\frac{{{x_1}+1}}{{{x_2}+1}}+1}}$①,
令$\frac{{{x_1}+1}}{{{x_2}+1}}=t(t>1)$,①式可化为$lnt=\frac{2(t-1)}{t+1}$
令$u(t)=lnt-\frac{2(t-1)}{t+1}$,$u'(t)=\frac{{{{(t-1)}^2}}}{{t{{(t+1)}^2}}}>0$,只需考查u(t)的值域即可.
解答 解:(1)x0f(x0)≥g(x0)可化为$a≤{x_0}^2-2ln{x_0}$,
令h(x)=x2-2lnx,则$h'(x)=\frac{2(x+1)(x-1)}{x}(x>0)$
∴当x∈$[\frac{1}{e},1)$时,h'(x)<0;当x∈(1,e]时,h'(x)>0;
又∵$h(\frac{1}{e})=\frac{1}{e^2}+2<h(e)={e^2}-2$,∴$h{(x)_{max}}={e^2}-2$,则a≤e2-2.…5分
(2)H(x)=x2+2ln(x+1)-1,$H'(x)=\frac{2}{x+1}+2x$;
$\frac{{H({x_1})-H({x_2})}}{{{x_1}-{x_2}}}=\frac{2}{{{x_1}-{x_2}}}ln\frac{{{x_1}+1}}{{{x_2}+1}}+({x_1}+{x_2})$;
$H'(\frac{{{x_1}+{x_2}}}{2})=\frac{4}{{{x_1}+{x_2}+2}}+({x_1}+{x_2})$;
故可化为$\frac{2}{{{x_1}-{x_2}}}ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{4}{{{x_1}+{x_2}+2}}$,即$ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{{2({x_1}-{x_2})}}{{{x_1}+{x_2}+2}}$…7分
又即$ln\frac{{{x_1}+1}}{{{x_2}+1}}$=$\frac{{2[({x_1}+1)-({x_2}+1)]}}{{({x_1}+1)+({x_2}+1)}}=\frac{{2[\frac{{{x_1}+1}}{{{x_2}+1}}-1]}}{{\frac{{{x_1}+1}}{{{x_2}+1}}+1}}$①,
令$\frac{{{x_1}+1}}{{{x_2}+1}}=t(t>1)$,①式可化为$lnt=\frac{2(t-1)}{t+1}$,…9分
令$u(t)=lnt-\frac{2(t-1)}{t+1}$,$u'(t)=\frac{{{{(t-1)}^2}}}{{t{{(t+1)}^2}}}>0$,∴u(t)在(1,+∞)上递增…11分
∴u(t)≥u(1)=0;∴u(t)无零点,故A、B两点不存在.…12分.
点评 本题考查导数的几何意义、运算及应用,涉及分离变量、构造函数、换元法以及转化思想,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 2$α+β=\frac{π}{2}$ | B. | 3$α+β=\frac{π}{2}$ | C. | 2$α-β=\frac{π}{2}$ | D. | 3$α-β=\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
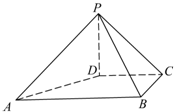 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,1) | B. | (-1,4) | C. | (-∞,-$\frac{3}{2}$) | D. | (-∞,$\frac{3}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com