
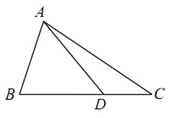
 如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.
如图,在△ABC中,AB=2,cosB=$\frac{1}{3}$,点D在线段BC上.分析 (1)求出sinB=$\frac{2\sqrt{2}}{3}$,由正弦定理得$\frac{AB}{sin∠ADB}=\frac{AD}{sinB}$,由此能求出AD.
(2)推导出S△ABD=2S△ADC,S△ABC=3S△ADC,${S}_{△ABC}=4\sqrt{2}$,BC=6,从而得到$\frac{sin∠BAD}{sin∠CAD}=2•\frac{AC}{AB}$,由此利用余弦定理能求出$\frac{sin∠BAD}{sin∠CAD}$的值.
解答 (本小题满分12分)
解:(1)在三角形中,∵cosB=$\frac{1}{3}$,∴sinB=$\frac{2\sqrt{2}}{3}$. …(2分)
在△ABD中,由正弦定理得$\frac{AB}{sin∠ADB}=\frac{AD}{sinB}$,
又AB=2,$∠ADB=\frac{π}{4}$,sinB=$\frac{2\sqrt{2}}{3}$.
∴AD=$\frac{8}{3}$. …(5分)
(2)∵BD=2DC,∴S△ABD=2S△ADC,S△ABC=3S△ADC,
又${S}_{△ADC}=\frac{4}{3}\sqrt{2}$,∴${S}_{△ABC}=4\sqrt{2}$,…(7分)
∵S△ABC=$\frac{1}{2}•AB•BC•sin∠ABC$,∴BC=6,
∵${S}_{△ABD}=\frac{1}{2}AB•AD•sin∠BAD$,${S}_{△ADC}=\frac{1}{2}AC•AD•sin∠CAD$,
S△ABD=2S△ADC,∴$\frac{sin∠BAD}{sin∠CAD}=2•\frac{AC}{AB}$,…(9分)
在△ABC中,由余弦定理得:
AC2=AB2+BC2-2AB•BC•cos∠ABC,∴AC=4$\sqrt{2}$,…(11分)
∴$\frac{sin∠BAD}{sin∠CAD}$=2•$\frac{AC}{AB}$=4$\sqrt{2}$. …(12分)
点评 本题考查线段长的求法,考查两个角的正弦值的比值的求法,是中档题,解题时要认真审题,注意正弦定理、余弦定理的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 215° | B. | 225° | C. | 235° | D. | 245° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{14}{15}$ | B. | $\frac{13}{15}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {0} | C. | {1} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
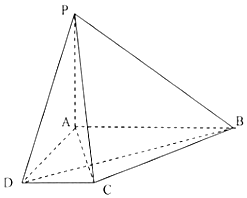 如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com