
分析 利用二倍角以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,求出函数的单调区间;在区间($\frac{π}{3}$,π)上有且仅有一个零点,可得$\frac{2π}{ω}$$≥π-\frac{π}{3}$,又因为$\left\{\begin{array}{l}{f(\frac{π}{3})<0}\\{f(π)>0}\end{array}\right.$,建立不等式关系,即可求实数ω的范围.
解答 解:函数f(x)=2cos$\frac{ωx}{2}$(sin$\frac{ωx}{2}$-$\sqrt{3}$cos$\frac{ωx}{2}$)+$\sqrt{3}$(ω>0)
化简可得:f(x)=2cos$\frac{ωx}{2}$sin$\frac{ωx}{2}$-2$\sqrt{3}$cos2$\frac{ωx}{2}$$+\sqrt{3}$=sinωx-$\sqrt{3}$cosωx=2sin(ωx$-\frac{π}{3}$).
周期T=$\frac{2π}{ω}$.
∵在区间($\frac{π}{3}$,π)上有且仅有一个零点,$\frac{2π}{ω}$$≥π-\frac{π}{3}$,可得ω≤3.
由$\left\{\begin{array}{l}{f(\frac{π}{3})<0}\\{f(π)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{sin(ω×\frac{π}{3}-\frac{π}{3})<0}\\{sin(πω-\frac{π}{3})>0}\end{array}\right.$,可得:$\left\{\begin{array}{l}{ω<1+3k}\\{ω>\frac{1}{3}+k}\end{array}\right.$,k∈Z,
∵ω>0,
当k=0时,可得:$\frac{1}{3}<ω<1$,
当k=1时,可得:$\frac{4}{3}<ω<4$;
∵ω≤3.
综上可得实数ω的范围为($\frac{1}{3}$,1)∪($\frac{4}{3}$,3].
故答案为($\frac{1}{3}$,1)∪($\frac{4}{3}$,3].
点评 本题主要考查三角函数的图象和性质的综合性运用能力,利用三角函数公式将函数进行化简是解决本题的关键.属于中档偏难题的题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
 右程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为24,39,则输出的a=( )
右程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为24,39,则输出的a=( )| A. | 2 | B. | 3 | C. | 4 | D. | 24 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{{\sqrt{7}}}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
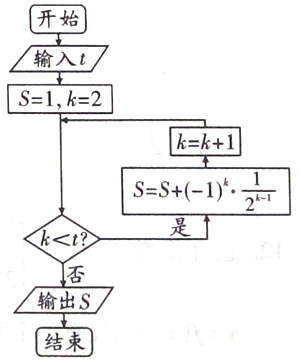
| A. | $\frac{11}{8}$ | B. | $\frac{9}{16}$ | C. | $\frac{5}{4}$ | D. | $\frac{21}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
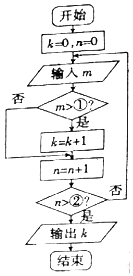 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是14,19.
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是14,19.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com