
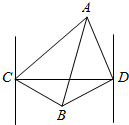
 如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号).
如图,一轮船自西向东匀速行驶,在C处测得A岛在东北方向,B岛在南偏东60°方向,此船向东航行6000海里后到达D处,测得A岛在北偏西15°方向,B岛在南偏西75°方向,则A,B两岛间距离为1000$\sqrt{42}$海里(结果保留根号). 分析 在△ABD中,求出AD,△CBD中,求出BD,△ABD中,求出AB即可.
解答 解:由题意,在△ABD中,∠ACD=45°,∠CAD=60°,CD=6000
∴由正弦定理可得$\frac{6000}{sin60°}=\frac{AD}{sin45°}$,∴AD=2000$\sqrt{6}$,
在△CBD中,∠CBD=135°,∠BCD=30°,CD=6000
∴由正弦定理可得$\frac{6000}{sin135°}=\frac{BD}{sin30°}$,∴BD=3000$\sqrt{2}$,
在△ABD中,∠ADB=90°,∴AB=$\sqrt{24000000+18000000}$=1000$\sqrt{42}$.
故答案为:1000$\sqrt{42}$.
点评 本题考查解三角形的实际应用,考查正弦定理的运用,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
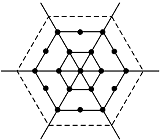 如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.
如图所示是一个有n层(n≥2,n∈N*)的六边形点阵,它的中心是一个点,算作第1层,第2层每边有2个点,第3层每边有3个点,…,第n层每边有n个点,则这个点阵共有( )个点.| A. | n2 | B. | n2+n | C. | 3n2-3n+1 | D. | 3n2-3n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (±$\sqrt{7}$,0) | B. | (0,±$\sqrt{7}$) | C. | (±5,0) | D. | (0,±5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com