
【题目】已知函数![]() ,
, ![]() .
.
(1)设![]() .
.
①若函数![]() 在
在![]() 处的切线过点
处的切线过点![]() ,求
,求![]() 的值;
的值;
②当![]() 时,若函数
时,若函数![]() 在
在![]() 上没有零点,求
上没有零点,求![]() 的取值范围;
的取值范围;
(2)设函数![]() ,且
,且![]() (
(![]() ),求证:当
),求证:当![]() 时,
时, ![]() .
.
科目:高中数学 来源: 题型:
【题目】从全校参加数学竞赛的学生的试卷中,抽取一个样本,考察竞赛的成绩分布,将样本分成![]() 组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为
组,绘成频率分布直方图,图中从左到右各小组的长方形的高之比为![]() ,最右边一组的频数是
,最右边一组的频数是![]() .
.
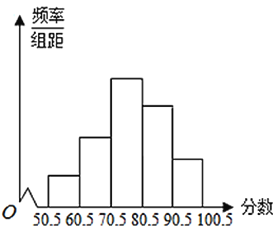
(1)成绩落在哪个范围的人数最多?并求出该小组的频数、频率;
(2)估计这次竞赛中,成绩高于![]() 分的学生占总人数的百分百.
分的学生占总人数的百分百.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,左顶点为
,左顶点为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条相互垂直的直线分别与椭圆
作两条相互垂直的直线分别与椭圆![]() 交于(不同于点
交于(不同于点![]() 的)
的)![]() 两点.试判断直线
两点.试判断直线![]() 与
与![]() 轴的交点是否为定点,若是,求出定点坐标;若不是,请说明理由.
轴的交点是否为定点,若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(卷号)2209028400021504
(题号)2209073114537984
(题文)
已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线在
时,求曲线在![]() 处的切线方程;
处的切线方程;
(Ⅱ)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(Ⅲ)对于曲线上的不同两点![]() 、
、![]() ,如果存在曲线上的点
,如果存在曲线上的点![]() ,且
,且![]() ,使得曲线在点
,使得曲线在点![]() 处的切线
处的切线![]() ,则称直线
,则称直线![]() 存在“伴随切线”. 特别地,当
存在“伴随切线”. 特别地,当![]() 时,又称直线
时,又称直线![]() 存在“中值伴随切线”.试问:在函数
存在“中值伴随切线”.试问:在函数![]() 的图象上是否存在两点
的图象上是否存在两点![]() 、
、![]() ,使得直线
,使得直线![]() 存在“中值伴随切线”?若存在,求出
存在“中值伴随切线”?若存在,求出![]() 、
、![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形,![]() ,
,![]() .
.
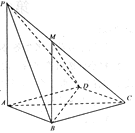
(Ⅰ)求证:直线![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正切值;
所成角的正切值;
(Ⅲ)设点![]() 在线段
在线段![]() 上,且二面角
上,且二面角![]() 的余弦值为
的余弦值为![]() ,求点
,求点![]() 到底面
到底面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
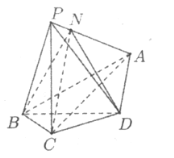
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,说明理由.
的长,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,对任意正整数n,皆满足
,对任意正整数n,皆满足![]() (实常数
(实常数![]() ).在等差数
).在等差数![]() (
(![]() ))中,
))中,![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)试判断数列![]() 能否成等比数列,并说明理由;
能否成等比数列,并说明理由;
(3)若![]() ,
,![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ,并计算:
,并计算:![]() (已知
(已知![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着“雾霾”天出现的越来越频繁,很多人为了自己的健康,外出时选择戴口罩,长郡中学高三兴趣研究小组利用暑假空闲期间做了一项对人们雾霾天外出时是否戴口罩的调查,共调查了120人,其中女性70人,男性50人,并根据统计数据画出等高条形图如图所示:
(Ⅰ)利用图形判断性别与雾霾天外出戴口罩是否有关系;
(Ⅱ)根据统计数据建立一个![]() 列联表;
列联表;
(Ⅲ)能否在犯错误的概率不超过0.05的前提下认为性别与雾霾天外出戴口罩有关系.
附: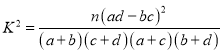

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com