【题目】过椭圆
的左焦点
作斜率为
的直线交椭圆于
，
两点，
为弦
的中点，直线
交椭圆于
，
两点.
（1）设直线的斜率为
，求
的值；
（2）若，分别在直线
的两侧，
，求
的面积.
【答案】（1）
（2）
【解析】
（1）设直线方程为
，代入椭圆方程，根据方程的根与系数关系求弦中点
的坐标为
，代入可得
，进行求解
（法二）（利用点差法）设点
，
，
，
，中点
，
，由
与
，作差得
再进行求解
（2）设直线方程为
，联立椭圆方程得出
，点的横坐标为
，用焦点弦公式表示出
，同理联立方程
，用弦长公式表示出
，
，结合题干
求出
，再用点到直线距离公式求得
到
距离，进而求得面积
（1）解法一：设直线方程为，代入椭圆方程并整理得：
，
，又中点在直线上，所以
，从而可得弦中点的坐标为，，
所以
解法二：设点，，，，中点， 则
，
，
又与，作差得
所以
（2）设
，
，
，
，点的横坐标为
于是
联立方程
所以
，
，
所以
从而有
，结合，
从而得
，不妨设
，此时
，
此时
，
科目：高中数学 来源： 题型：
【题目】如图，
是边长为2的正方形，平面
平面，且
，
是线段
的中点，过
作直线
，
是直线
上一动点.
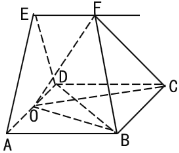
（1）求证：
；
（2）若直线上存在唯一一点使得直线
与平面
垂直，求此时二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】给出如下四种说法：
①四个实数
依次成等比数列的必要而不充分条件是
.
②命题“若
且
，则
”为假命题.
③若
为假命题，则
均为假命题.
④若数列
的前项n和
，则该数列的通项公式
.
其中正确说法的序号为________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某电动汽车“行车数据”的两次记录如下表：
记录时间 | 累计里程 （单位：公里） | 平均耗电量（单位： | 剩余续航里程 （单位：公里） |
2019年1月1日 | 4000 | 0.125 | 280 |
2019年1月2日 | 4100 | 0.126 | 146 |
（注：累计里程指汽车从出厂开始累计行驶的路程，累计耗电量指汽车从出厂开始累计消耗的电量，平均耗电量=
，剩余续航里程=
，下面对该车在两次记录时间段内行驶100公里的耗电量估计正确的是
A. 等于12.5B. 12.5到12.6之间
C. 等于12.6D. 大于12.6
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲船在岛
的正南
处，以4千米/时的速度向正北方向航行，
千米，同时乙船自岛出发以6千米/时向北偏东60°的方向驶去.当甲、乙两船相距最近时，它们所航行的时间为（ ）
A.
B.
C.
D.2.15h
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】将参加夏令营的600名学生编号为：001，002，…，600，采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003．这600名学生分住在三个营区，从001到200住在第一营区，从201到500住在第二营区，从501到600住在第三营区，三个营区被抽中的人数依次为（ ）．
A.16，26，8B.17，24，9C.16，25，9D.17，25，8
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我国是世界上严重缺水的国家，某市为了制定合理的节水方案，对居民用水情况进行调查，通过抽样，获得某年100为居民每人的月均用水量（单位：吨），将数据按照
分成9组，制成了如图所示的频率分布直方图.
（1）求直方图的
的值；
（2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，说明理由.
（3）估计居民月用水量的中位数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系中，以原点为极点，x轴的正半轴为极轴，以相同的长度单位建立极坐标系．己知直线
的直角坐标方程为
，曲线C的极坐标方程为
．
（1）设t为参数，若
，求直线的参数方程和曲线C的直角坐标方程；
（2）已知：直线与曲线C交于A，B两点，设
，且
，
，
依次成等比数列，求实数a的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
