
分析 分别求出p,q为真时的m的范围,根据若p∧q为真命题,取交集即可.
解答 解:函数$f(x)={2^{{x^2}-2x}}+{m^2}-\frac{5m}{2}+\frac{1}{2}$在R上有零点,
即-${2}^{{x}^{2}-2x}$=m2-$\frac{5m}{2}$+$\frac{1}{2}$有解,
令g(x)=-${2}^{{x}^{2}-2x}$≤-$\frac{1}{2}$,
故m2-$\frac{5m}{2}$+$\frac{1}{2}$≤-$\frac{1}{2}$,
解得:$\frac{1}{2}$≤m≤2;
故p为真时:m∈[$\frac{1}{2}$,2];
函数f(x)=$\frac{2}{x-m}$在区间(1,+∞)内是减函数,
则m≤1,
若p∧q为真命题,则p真q真,
故$\frac{1}{2}≤m≤1$,
故答案为:[$\frac{1}{2}$,1].
点评 本题考查了复合命题的判断,考查指数函数以及二次函数的性质,是一道中档题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
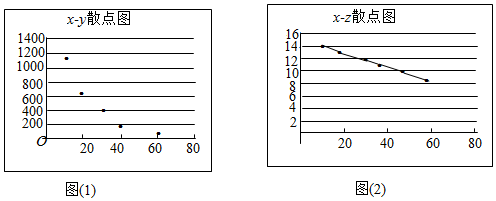
| 定价x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| z=2lny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com