
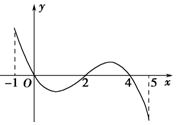
 ��֪����f��x���Ķ�����Ϊ[-1��5]�����ֶ�Ӧֵ���±���f��x���ĵ�����y=f�䣨x����ͼ����ͼ��ʾ�����й���f��x�������⣺
��֪����f��x���Ķ�����Ϊ[-1��5]�����ֶ�Ӧֵ���±���f��x���ĵ�����y=f�䣨x����ͼ����ͼ��ʾ�����й���f��x�������⣺| A�� | �٢� | B�� | �٢ڢ� | C�� | �٢ڢ� | D�� | �٢ڢۢ� |
���� �ɼ�ֵ��Ķ��弴���жϢ٣��ɵ����ķ��ţ������жϵ������䣬�жϢڣ�
�ɼ���ֵ����Ϊ���ֵ�������жϢۣ���ת��˼��ɵ�f��x��=a��ͼ�������������������ֵ�н�СΪa����һ������a�������жϢܣ�
��� �⣺�ٹ۲쵼����ͼ��ɵ�f�䣨x����x=0��x=4�������Ҹ���ȡ�ü���ֵ���ʢ���ȷ��
�ں���f��x���ڣ�0��2���ĵ���Ϊ���ģ���f��x��������[0��2]���Ǽ��������ʢ���ȷ��
�������x��[-1��t]ʱ��f��x�������ֵ��2��������f��0��=2��f��4��=2����ôt�����ֵΪ5��
�ʢ۴���
�ܵ�1��a��2ʱ������y=f��x��-a����f��x��=a��ͼ������ɵ���������
��f��x����һ������ֵΪa����һ������ֵ����aʱ���ɵ��������������㣬��������㣮
�ʢܴ���
���Ͽɵã��٢���ȷ��
��ѡ��A��
���� ���⿼�麯���ĵ��������ã���ֵ����ֵ���Լ��������䣬ע��ͨ��ͼ��۲죬�Լ�ת�����ж��������������ν��˼�뷽���������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֱ�����ɵĽǷ�Χ��[0����] | |
| B�� | ���⡰?x��R��2x��0���ķ��ǡ�?x��R��2x��0�� | |
| C�� | ��p��qΪ�����⣬��p��q��Ϊ������ | |
| D�� | x2��1������һ����ֶ�����Ҫ��������x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x������ƽ��$\frac{��}{2}$����λ���������쳤Ϊԭ����2�� | |
| B�� | ��x������ƽ��$\frac{��}{2}$����λ���������쳤Ϊԭ����2�� | |
| C�� | ��x������ƽ��$\frac{��}{4}$����λ���������쳤Ϊԭ����2�� | |
| D�� | ��x������ƽ��$\frac{��}{4}$����λ���������쳤Ϊԭ����2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com